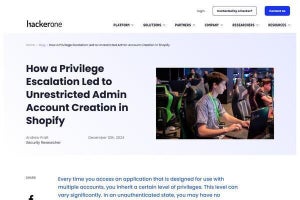
オープンループ型MIMO
単一の送信アンテナを使うシステム、すなわちSIMO (Single-input and Multiple-output)の場合、受信側(Rx)は最大比合成(MRC:Maximal Ratio Combining)技術を利用して、複数の受信アンテナで取得したデータ・ストリームを合成し、ダイバーシティ利得を得る。
一方、送信アンテナを複数使用するシステムの場合は、チャネルの複雑性が増すため複数の送信データ・ストリーム間で干渉を引き起こす。チャネルに関する情報を送信側(Tx)が保有していなければ、受信側(Rx)が単独でMIMOのキャパシティを引き出さなければならなくなり、通常は複雑なアルゴリズムが必要になる。
空間多重化伝送(Spatial Multiplexing)
空間多重化伝送は、オープンループ型MIMOを実現する1つの方式として知られており、無線通信システムで広く採用されている。空間多重化伝送では、送信アンテナがそれぞれ異なるデータ・ストリームを送信する。2×2の空間多重化伝送システムを示したのが図1だ。このシステムは次の式で表すことができる。
|
|
ここで、xは送信信号ベクトル、Hはチャネル行列、nは付加雑音ベクトル、yは受信信号ベクトルと定義する。受信信号yから送信信号xを推測する最も簡単な方法は、ゼロ・フォーシング(ZF:Zero Forcing)検出法や、最小平均2乗誤差(MMSE:Minimum Mean Squared Error)法などで、いずれもyにチャネル行列の逆数を掛ける方法だ。しかしながら、これは最適検出法ではない。
最適検出法とは、最尤(ML:Maximum Likelihood)基準に則った方法だ。多くの場合、ユークリッド距離が受信信号ベクトルyに対して最短となる送信信号ベクトルを求めることで、ML基準に則った数値を得ることができる。
|
|
しかしながら、この検出法では、送信アンテナや配置点の数にしたがって複雑性が指数関数的に増すことになり、このため、実用的なシステムにML基準を用いるのは適切ではない。
そこで、準最適なML検出法として広く採用されているのが球面復号化(Sphere Decoding)だ。球面復号化アルゴリズムの原理は、格子フィールドの格子点に各符号後(コードワード)を割り当てた球体の半径内において、受信信号に最も近い格子点を検出するというもの。球体復号化を使えば、複雑性は大幅に軽減されるため、パフォーマンス面でもML検出法とそれ程差異はなくなる。
しかしながら、球面復号化を使えば複雑性は軽減されるが、アンテナ数が多い場合や、64値QAM(Quadrature Amplitude Modulation)といった変調速度が高い変調方式を採用した場合では適切な方法とは言えない。