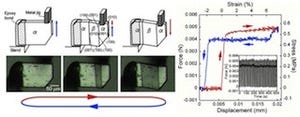
具体的には、最も基本的な遊泳の数理モデルである「パーセル・スイマー」に奇弾性が導入され、流体計算が行なわれた結果、自律的な遊泳挙動が現れることが発見されたという。奇弾性体の内的なゆらぎがスイッチのように働き、しなやかな遊泳運動が自発的に生まれることが示されたとする。
また、この挙動の背後に潜む仕組みの解明に挑んだところ、マクスウェル・ベッチの非相反性と、帆立貝定理に現れる変形の非相反性は、まったく異なる2つの概念だが、両者を結びつけるというアイデアが研究の鍵となり、これらはいずれも、物体の形状を表現する形状空間内の確率的な流れとして表現できることが見出されたという。
さらに、形状空間を表現する曲がった空間の幾何学を用いることにより、奇弾性体の遊泳公式を導くことにも成功したとする。この遊泳公式により、自発的な遊泳が奇弾性そのものに起因していることを証明することが可能となったとする。研究チームでは、このようなゆらぎを伴う物理現象は非平衡統計力学の研究分野で活発に研究されていたが、今回の研究は、その概念と手法を、流体と弾性体の遊泳問題に持ち込んだ画期的な枠組みになっていると説明する。
これらの結果は、奇弾性という新しい物質観によって、さまざまな生体現象や自発現象を統一的に理解できる可能性を示すもので、このようなアプローチは、多様で複雑な生体現象に対してある種の普遍性を発見することにつながり、基礎理論の大きな発展をもたらすものだという。
なお、今後については、これらの奇弾性率を現実の系で見積もり、実際の微生物などがどの程度の大きさの奇弾性を持っているかを調べる予定としているほか、体内を移動する自律型マイクロマシンの設計についても、今回の研究の遊泳公式は応用可能としている。
また、今回の弾性体の遊泳の基本原理は、自律的なマイクロマシンの開発と実現に向けて、基礎と応用の両面における貢献が期待されるとしているほか、この奇弾性による大胆な試みは新しい科学や技術の発展の礎となるものだともしている。