計算処理のアクセラレータと言えば、GPUかIntelのXeon Phi(MIC)であるが、どちらを使うのが良いのかという情報が無く選択に迷うということが多い。これに関して、首都大学東京が主催する「メニーコアステムにおける格子アプリケーション -GPUとMICの実行性能比較-」と題するミニ研究環ワークショップが開かれた。
東工大 青木教授の7点ステンシル計算での性能比較
このワークショップにおいて、共催者でもある東京工業大学(東工大)の青木尊之教授は、「7点ステンシル計算(拡散方程式)に対するGPUとMICの実行性能比較」と題して発表を行った。
拡散の計算は、左の図のように、一点に染料を垂らした場合にそれがどのように広がっていくかを求めるような計算である。これをコンピュータで計算する場合は、全体を格子に区切り、計算の対象となる格子とそれに隣接する6つの格子の状態(計7点の値)から、対象の格子の次の状態を計算する。これをすべての格子を対象として計算し、それを使って、また、次の時点のすべての格子の状態を計算するという処理を繰り返す。右の図のプログラムの最後の4行がこの計算を行っている部分である。
この計算は状態f[ ] に係数を掛けて合計を求めるという処理で、7個のf[ ]をメモリから読み、13回の演算を行い、結果をメモリに書き込んでいる。
この計算を実行するときの性能は、処理に必要な演算数をFLOP、必要なメモリアクセス量をByteとし、実行するハードウェアのピーク演算性能をF、ピークメモリバンド幅をBとすると、次の左の図のように表される。Performanceの式の右辺の分母は演算時間(FLOP/F)とメモリアクセス時間(Byte/B)とその他の時間αの和となっている。合計の時間で演算数FLOPを割るとFlop/sの性能になるという式になっている。
この式を変形すると、右の図のようになり、ハードウェアを決めると、あとはFLOP/Byteの値で性能が決まることになる。ここで7点ステンシル計算のFLOPは13演算で、Byteはすべてのメモリアクセスが実際にメモリをアクセスすると想定すると8回で、単精度の浮動小数点データとすると8×4バイトとなる。一方、メモリアクセスが最大限キャッシュにヒットすると考えると、対象とする格子のデータの読み込みと書き出しの2回のメモリアクセスで済み2×4バイトとなる。そして、FLOP/Byteは、前者の場合0.406、後者の場合1.625と計算される。
|
|
|
|
処理に必要な演算数(FLOP)とアクセスするメモリ量(Byte)とハードウェアのピーク演算性能F、ピークメモリバンド幅Bから性能を見積もるRooflineモデル |
式を変形すると、処理のFLOP/ByteとハードウェアのF/B(B/F比の逆数)で性能を表す式になる |
次の図はXeonと各種のGPUの性能がFLOP/Byteでどう変化するかを示す図で、αがゼロの理想的な状態でも、これ以上の性能は出ないという上限の線を書いたものである。このモデルを「Roofline Model」という。
この図の重要な点は、FLOP/Byteが6.96以下の場合はメモリバウンド(メモリアクセス時間が律速)、それ以上の場合は演算時間が律速ということが分かるということである。つまり、7点ステンシル計算の場合は、理想的にキャッシュにヒットしてもメモリバウンドの問題であるということが分かる。
右の図は、各種GPUとXeon Phiのメモリバンド幅を測定した結果で、横軸はメモリアクセスのバイト数である。ビジーな図であるが、一番下のグラフが「Xeon E5 2670 CPU」で、その上の階段状の2本の線がXeon Phiで、性能の低い方は3110で、高い方は5110Pの結果である。
このグラフを見ると、メモリバンド幅では、Xeon PhiはNVIDIAのGTX Titanなどに大きく差を付けられている。
|
|
|
|
Roofline Modelを見ると、その計算がメモリアクセス律速か演算律速かが分かり、実測値が限界にどれだけ近いかが分かる |
CPU、Xeon Phiと各種GPUのメモリバンド幅の実測値。一番下がCPU、その上の階段状の2本の線がXeon Phi。それ以外はGPU |
7点ステンシル計算をXeon Phiで実行する場合、前述のソースコードに#pragma omp parallelなどの簡単なディレクティブで並列化を指定しただけの場合は、実行性能は80.2GFlopsであったという。これを境界条件のチェックの部分をループの外に出すX方向のピーリングを行うようにソースコードを変形すると105GFlopsに上がった。さらにブロックごとに計算してキャッシュのヒット率を改善するY方向のタイリングを行うと112GFlopsとなったという。
一方、GPUの場合はレジスタを使ってZ方向のメモリアクセスを減らす、シェアードメモリを使ってX方向のメモリアクセスを減らす、そして、Temporal Blocking という手法を使って、時間方向でメモリアクセス回数を減らすという手法を適用した。
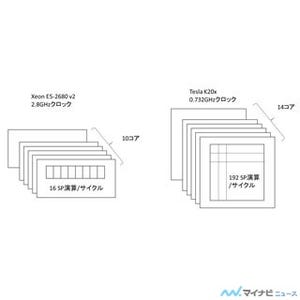
次の左の図の棒グラフは7点ステンシル計算の性能を示すもので、左から順に「Xeon E5 2670 CPU」、「Xeon Phi 5110P」、「Tesla M2050」、「Tesla K20c」、「Tesla K20x」、「GeForce GTX Titan」、「GeForce GTX Titan Black」、「GeForce GTX980」のデータで、それぞれの棒は前述の改善を加えて行ったときの各ステップでの性能を表している。
このグラフから、実効メモリバンド幅の小さいXeon PhiはGPUに比べて性能が低く、Tilingでメモリアクセス回数を減らすと大きく性能が上がっていることがわかる。フェルミアーキテクチャのM2050はL1キャッシュが効いていてすでに性能が上がっているためか,色々な手法を使ってもあまり性能は上がらなかったが,それ以外のGPUでは,チューニングにより,かなりの性能向上が得られている。
右側の図は、FLOP/Byteが1.6の拡散方程式(7点ステンシル計算)とより計算が複雑でFLOP/Byteが9.8の圧縮流体の計算をGPUとXeon Phiで行った場合の性能をRoofline Modelの図にプロットしたもので、前者はメモリ律速の計算で、後者は演算律速の処理である。どの結果も上限の線からは多少下がった性能となっているのは当然であるが、演算律速の圧縮流体の計算では、Xeon Phiの実効バンド幅が小さいということが問題にならないので限界性能との差が小さくなっている。