2016年6月8日に理化学研究所(理研)で、「スーパーコンピュータHOKUSAIとShoubu、研究の最前線」と題するシンポジウムが行われ、電気通信大学(電通大)の山﨑匡 助教が「Shoubuで実現するネコ一匹分の人工小脳」と題する招待講演を行った。なお、Shoubuでの実装は始めたばかりであるため、今回の発表は小脳の話とShoubuへの実装の話に留まり、Shoubu上の人工小脳で何ができるのかは話せる状態になっていないという。
小脳とはどんなものなのか?
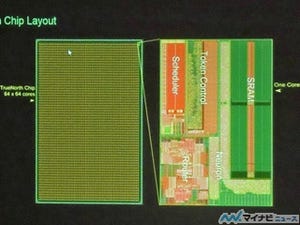
山﨑氏は小脳を研究しておられ、GPU版の人工小脳を作っており、それを元に運動記憶が定着することを示した。視野像をゆっくりと左右に動かすと眼球も同じ方向に回転するが、このトレーニングを繰り返すとより大きく回転し視野の動きにより良く追従できるようになる。GPUで作った人工小脳でも、次の図の右下のグラフのように練習を重ねるに従って回転がより大きくなるという現象が再現できたという。
|
|
|
チェッカーパターンを眼前で動かして、それを追う目の動きが、学習によって大きくなるという現象を人工知能でも再現した (この連載のすべての図は,理研シンポジウムにおける山﨑氏の発表スライドのコピーである) |
また、山﨑氏の研究はリアルタイムで処理ができる人工小脳であるので、ボールを打ち返すというような学習ができる。最初は振り遅れていたが、しばらく学習するとピッチングマシンが投げる瞬間の信号から、どれだけの遅れでバットを振れば良いかを学習したという。
人間には大脳と小脳があるが、体積で言うと大脳が80%で小脳は10%であるが、細胞の数でいうと大脳は19%、小脳は80%で、圧倒的に小脳の細胞数が多い。
大脳の神経ネットワークは多階層で、比較的少数の細胞を階層的に積み、徐々に次元を削減していく情報処理を行っていると考えられるが、小脳のネットワークは3層の浅いネットワークで、一度高次元空間上に写像し、その上で情報処理を行うという、細胞数にものを言わせた力任せの計算を行っていると考えられる。小脳のネットワークは浅いので、多層ネットワークを使う大脳よりも処理遅延時間が短く、反射的な反応に都合が良いという。
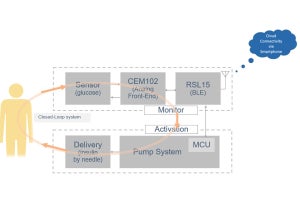
大脳の高次運動野からの、手足などをこう動かせという目標軌道に対して、1次運動野がそれを運動指令に変換して、手足を動かす指令を送る。そして実現された動きを感覚系がフィードバックして、目標の動作に近づける。この系は遅延が無ければ上手く動くが、遅延があると制御が遅れてしまい発振したりしてしまう。
小脳は、運動指令から体の動きを予測してフィードバックをかける。このフィードバックは遅れが小さいので、感覚系のフィードバックを使わずに済み、発振せず安定に動作する。
また、小脳は一次運動野の働きを行い、その誤差を学習して、身体部位への運動指令の誤差を小さくするという働きも持っていると考えられる。
小脳のニューロンネットワークは3層で、第1層は橋核と呼ばれる細胞で、ここに触覚、痛覚、聴覚、視覚などの各種センサからの入力が入ってくる。また、大脳からの信号もここに入っている。
そして苔状線維で、第1層の橋核から第2層の顆粒細胞に繋がっている。この接続は疎でそれぞれの顆粒細胞には一部の橋核からしか繋がっていない。一方、第2層の顆粒細胞から第3層のプルキンエ細胞の間は平行線維でつながっており、この接続はかなり密である。
さらに、プルキンエ細胞の出力は小脳核で総合される。また、下オリーブ核はプルキンエ細胞の教師として働くと考えられている。
ニューロンは短いパルス信号(スパイク)で動作する。スパイクがシナプスに到着すると、シナプス後膜の電位が上がり、それが受け手のニューロンに伝わる。複数のシナプスからの電位の合計が、ある閾値を超えるとニューロンがスパイクを出力するというように動作する。
この動作は、次の図の膜電位を表す微分方程式と、コンダクタンスの式で表すことができる。従って、この式を計算することでニューロンの動きをシミュレートすることができる。入力数がNの場合、N本の膜電位の式と、3N本のコンダクタンスの式を1msのステップで計算して行く。