ゼロからはじめてみる日本語プログラミング「なでしこ」(83) フィボナッチ数列を名画と重ねてみよう

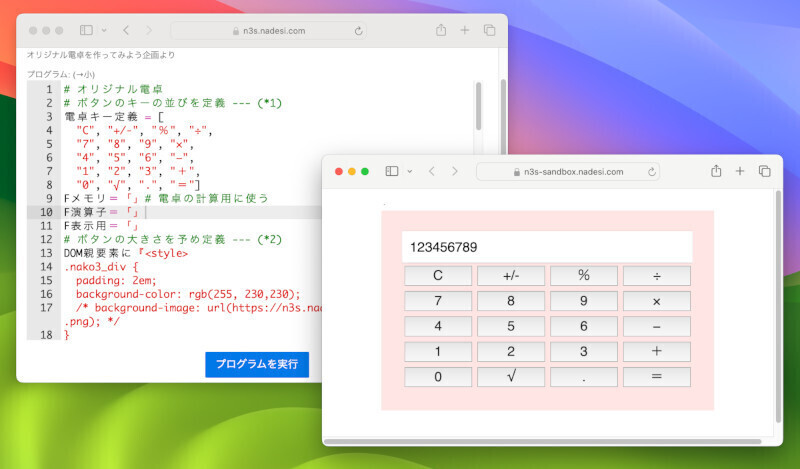
「フィボナッチ数列」というのは、全ての要素が前にある2つの数値を足した値になる数列のことです。このフィボナッチ数列は自然界に多く見られる数列であり、さまざまな芸術やデザインにも応用されています。なでしこを使って数列を作成し実際に描画して確かめてみましょう。

フィボナッチ数列を元にして描いた図形を名画に重ねたところ

フィボナッチ数列とは？

フィボナッチ数列というのは、1,1,2,3,5,8,13,21…のように、全ての要素について、前2つの数値を足したものが次の要素の値になっている数列のことです。これは、13世紀イタリアの数学者フィボナッチが紹介したものです。1つがいのウサギが次々と増えていく様子を元にしてこの数列を考案しました。

この数列が人々の興味を引く点ですが、自然界に現れるさまざまな数字とぴったり一致しているという点です。例えば、ヒマワリの種の数、ハチやアリなどの家系、植物の花や実に現れる螺旋の数などが、フィボナッチ数列に一致しています。加えてフィボナッチ数列は美しいデザインに欠かせないもので、さまざまなデザインに応用されています。

フィボナッチ数列を作成しよう

それでは、実際になでしこのプログラムを作って、フィボナッチ数列作成を作成してみましょう。前にある2つの値を足した値が次の値になるのですから、繰り返し構文を使うことで簡単に作成できます。

例えば、次のような関数を定義できるでしょう。なでしこ簡易エディタに以下のプログラムを入力してみましょう。

●(作成個数の)フィボナッチ数列作成とは：
　　前値=1
　　次値＝1
　　結果=[前値,次値]
　　1から(作成個数-2)まで繰り返す：
　　　　値＝前値＋次値
　　　　結果に値を配列追加。
　　　　前値＝次値
　　　　次値＝値
　　結果を戻す
30のフィボナッチ数列作成して表示。

プログラムを実行すると次のように表示されます。画面の下に、「1,1,2,3,5,8,13,21,34,55,89,144,233…」とフィボナッチ数列が表示されます。

フィボナッチ数列を作成して表示したところ

フィボナッチ数列を描画してみよう

なでしこで数列をグラフにするには、数列を二次元配列に変換することで手軽に描画が可能です。

先ほど作った関数「フィボナッチ数列作成」のすぐ下に、以下のコードを書き足して、プログラムを実行してみてください。

結果＝[["フィボナッチのグラフ"]]
25のフィボナッチ数列作成して反復：
　　結果に[対象]を配列追加
結果を線グラフ描画。

同じように簡易エディタで実行すると次のようにグラフが描画されます。

線グラフにしたところ

このようにグラフで確認してみると、フィボナッチ数列がどのようなものなか視覚的に確認できるでしょう。

タートルお絵かきでフィボナッチを描画してみよう

次に、タートルグラフィックスで、フィボナッチ数列に合わせて図形を描画してみましょう。フィボナッチ数列に合わせて正方形を描きます。以下のプログラムは、5個分のフィボナッチ数列を計算して、それを螺旋状に配置したものです。

こちらは、描画キャンバスのサイズが指定できる、なでしこ貯蔵庫で試してみましょう。エディタ右下でキャンバスサイズを指定できますので、800x800に設定した上で実行してみてください。

# フィボナッチ数列を取得 --- (*1)
F数列=5のフィボナッチ数列作成。
# 描画パラメータを指定 --- (*2)
拡大率=10; X=100; Y=100; 開始角度=0
カメ作成。
2にカメペンサイズ設定
2にカメ速度設定。
「#33AA44」にカメペン色設定
# カメを使ってフィボナッチ数列を描画 --- (*3)
[X,Y]にカメ起点移動。
開始角度だけカメ右回転
F数列を反復：
　　N=対象×拡大率
　　4回:
　　　　Nだけカメ進む
　　　　90だけカメ右回転
　　Nだけカメ進む。
　　90だけカメ右回転
　　Nだけカメ進む。

●(作成個数の)フィボナッチ数列作成とは:
　　前値=1; 次値＝1
　　結果=[前値,次値]
　　1から作成個数まで繰り返す：
　　　　値＝前値＋次値
　　　　結果に値を配列追加。
　　　　前値, 次値＝[次値, 値]
　　結果を戻す

プログラムを実行してみると、次のように表示されます。

タートルグラフィックスでフィボナッチ数列作成を描画した

プログラムを確認してみましょう。(＊1)ではフィボナッチ数列を5要素分作成します。そして、(＊2)では描画パラメータを指定します。座標や色を指定しています。そして、(＊3)で実際の描画を行います。読んだとおり、フィボナッチ数列の各値を、拡大率分だけ大きくして、その値に従って正方形を描きます。これによって、上記のような図形が描画できます。

芸術作品にフィボナッチ数列を重ねてみよう

なお、フィボナッチ数列を元にして描画した上記の図形は、とても面白いものとなっています。隣り合う正方形のサイズを比べてみると「黄金比(1:1.618=5:8)」になっているのです。

黄金比というのは、人間の美的感覚から「美しい」と感じる比率です。自然界に見られる多くの美しい景観が、このフィボナッチ数列に沿っているというのは、とても偶然とは思えません。

そして、このフィボナッチ数列を名画に重ねてみると、それらがピッタリはまることが分かります。レオナルド・ダ・ヴィンチの「モナリザ」や葛飾北斎の「冨嶽三十六景神奈川沖浪裏」など、ピッタリとハマりますので実際に試してみましょう。

まずはモナリザで試してみましょう。以下のプログラムも貯蔵庫でキャンバス幅を800x800に設定して試してみてください。

# フィボナッチ数列とモナリザ
# パラメータを指定 --- (*1)
モナリザURL=「https://n3s.nadesi.com/image.php?f=469.jpg」
拡大率=25; X=215; Y=230
カメ作成
0にカメ速度設定
3にカメペンサイズ設定
黄色にカメペン色設定
# 画像を読み込む --- (*2)
IMG=モナリザURLの画像読み待つ。
IMGを[0,0,535,800]に画像描画。
# 描画開始 --- (*3)
[X,Y]にカメ起点移動。
F数列=5のフィボナッチ数列作成。
F数列を反復：
　　N=対象×拡大率
　　# 正方形を描画
　　4回:
　　　　Nだけカメ進む
　　　　90だけカメ右回転
　　# 正方形を分断する線を描画
　　NN=SQRT(N*N+N*N)
　　45だけカメ右回転;
　　NNだけカメ進む; NNだけカメ戻る
　　45だけカメ左回転
　　# 正方形が重ならないようカメを進める
　　Nだけカメ進む。
　　90だけカメ右回転
　　Nだけカメ進む。
●(作成個数の)フィボナッチ数列作成とは:
　　前値=1
　　次値＝1
　　結果=[前値,次値]
　　1から作成個数まで繰り返す：
　　　　値＝前値＋次値
　　　　結果に値を配列追加。
　　　　前値＝次値
　　　　次値＝値
　　結果を戻す

プログラムを実行すると次のようにモナリザの画像に重ねて、フィボナッチ数列の図形を描画します。どうでしょう！鼻、顔、手の位置がフィボナッチ数列を元に描いた図形にぴったりハマっています。フィボナッチ数列が芸術に適用されているお手本のような絵画です。