iPadを使って二人で遊べるリバーシを作ってみよう

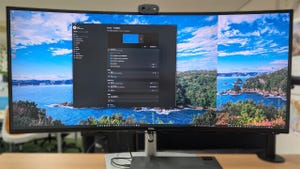
なでしこ3を使うと、iPadなどタブレットで動くプログラムも手軽に作成できます。今回は、iPadなどタブレットで使うことを念頭にしつつ、二人で遊べるテーブルゲームの定番、リバーシを作ってみましょう。

• iPadでリバーシゲームを実行しているところ

テーブルゲームの定番「リバーシ」とは？

リバーシとは、二人のプレイヤーが交互に白と黒の石を盤面に起きながら進めるテーブルゲームです。相手の色の石を自分の色で挟むことで、自分の色の石に変えていきます。そして、最終的に盤上の色が多い方が勝利となります。有名なゲームなので、これ以上の詳しいルールの説明は不要でしょうか。

休日に家族と二人でゆっくり遊べるリバーシを作ろう

ルールが単純なことから、リバーシは、コンピューターゲームとしても、古くから作られています。一般的にコンピューター上で遊ぶ場合、一人用のものが大半です。コンピューターのAIが相手になってくれます。AIの性能によって、強かったり弱かったりします。

もちろん、プログラムを作って楽しいのは、対戦相手のAIをどのように実装するのかという点なのですが、今回は「夏休みや休日に家族と対戦する」というテーマの元、AIは作らない方針でいきましょう。

そのため、黙々とリバーシのルールだけを実装するのですが、それでも、なでしこで160行ほどのプログラムを書く必要があります。この長さだと、ちょっと頭をひねる必要があるでしょうか。

最初にどんなものを作るのか実際のプログラムを確認してみましょう。今回のプログラムは、なでしこ3貯蔵庫（こちら）に投稿してあります。

• 二人対戦リバーシがすぐに実行できる

リバーシのプログラムの作り方

それでは、一つずつプログラムを作っていきましょう。まず、最初に考えるべきことは、リバーシのゲームをどのようなデータ構造で表現するのかという点です。以前、連載の65回目でトランプゲームを作った時にも解説しましたが、データ構造をうまく設計できると、プログラムを単純にすることができます。

リバーシの場合は、縦横8×8のマスの盤面が登場し、そこに白と黒の石を配置することになります。この時、8×8の盤面は、二次元配列変数を使って表現すると良いでしょう。

それで、盤の1マスを数値で表現し、0であれば石なし、1であれば黒の石、2であれば白の石と表現することにします。リバーシの初期盤面を表現するように次のような関数を用意できるでしょう。

●盤面初期化とは
　盤面=[
　　[0,0,0,0,0,0,0,0],
　　[0,0,0,0,0,0,0,0],
　　[0,0,0,0,0,0,0,0],
　　[0,0,0,2,1,0,0,0],
　　[0,0,0,1,2,0,0,0],
　　[0,0,0,0,0,0,0,0],
　　[0,0,0,0,0,0,0,0],
　　[0,0,0,0,0,0,0,0]
　]
ここまで。

ここまで決めたら、リバーシの盤面を描画することができるでしょう。上記の関数を利用しつつ、盤面を描画するプログラムが次の通りです。

# データを初期化
タイル幅＝37
F黒=1。F白=2。
盤面=[]。
盤面初期化。
盤面描画。

●盤面描画とは
　　全描画クリア。
　　1に線太さ設定。黒色に線色設定。
　　# 左上から右下へ繰り返し盤面を描画する --- (*1)
　　Yを0から7まで繰り返す
　　　　Xを0から7まで繰り返す
　　　　　　# 石のない空白マスを描画 --- (*2)
　　　　　　XX=X×タイル幅
　　　　　　YY=Y×タイル幅
　　　　　　緑色に塗り色設定。
　　　　　　[XX,YY,タイル幅,タイル幅]へ四角描画。
　　　　　　# 白黒の石を描画 --- (*3)
　　　　　　R=タイル幅÷2
　　　　　　もし、盤面[Y,X]=F白ならば
　　　　　　　　白色に塗り色設定。
　　　　　　　　[XX+R,YY+R]へ(R-3)の円描画。
　　　　　　違えば、もし、盤面[Y,X]=F黒ならば
　　　　　　　　黒色に塗り色設定。
　　　　　　　　[XX+R,YY+R]へ(R-3)の円描画。
　　　　　　ここまで。
　　　　ここまで。
　　ここまで。
ここまで。
# ... ここに盤面初期化をコピーする ...

なでしこ貯蔵庫で右上の「新規」ボタンを押して、そこに上記のプログラムを記述して実行すると、次のようにリバーシの盤面が描画されます。

• リバーシの盤面を描画したところ

上記のプログラムのポイントを確認してみましょう。まず、(＊1)の部分で、左上から右下へと盤の1マスを1つずつ描画していきます。そのために「繰り返す」構文を二重で使って、Y方向とX方向と満遍なく描画します。

(＊2)の部分では、実際に描画を行う座標(XX, YY)を計算し、「四角描画」を使って緑色の盤を描画します。(＊3)では変数「盤面」の内容を確認して石を描画します。

石が置けるのか判定する

そして、今回最も重要な処理となるのが、石を置けるのか判定する処理です。石が置けるかどうかの条件を確認してみましょう。