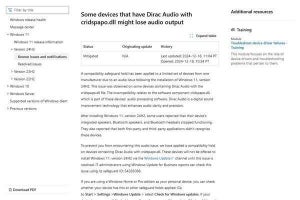
サンプル調査によりデータを収集した場合は、その平均値に「どれくらいの信頼性があるか？」を検証しておくのが基本だ。そこで今回は、平均値の信頼性を確認する「95％信頼区間」の算出方法を紹介していこう。

平均値の95％信頼区間

今回も具体的な例を使って解説していこう。以下の図は、ある菓子メーカーが「1袋に詰めるスナック菓子の量」を決定するために、10名の協力者に新商品を好きなだけ食べてもらい「十分に満足した量」をまとめたサンプル調査となる。

  • サンプル調査の結果

前回の連載でも解説したように、このサンプル調査の標本平均は81.33（g）という結果になった。では、この81.33（g）という数値は、どれくらい信頼できる指標といえるだろうか？

標本平均はあくまで「10名のサンプルの平均」を算出したものでしかなく、必ずしも母集団の平均値（母平均）に一致するとは限らない。むしろ、多少の誤差を含んでいると考えるのが自然だ。

もしかすると、10名の協力者の中に大食いの人が多くいたため、母平均より大きな数値になっている可能性も考えられる。逆に、少食の協力者が多かったため、母平均より小さな数値になっている可能性もある。

そこで、統計学では「95％信頼区間」と呼ばれる手法を使って「平均値の信頼性」を推測する。「平均値の95％信頼区間」は、

　△△～△△の範囲に母平均が95％の確率で含まれる

ということを示したものだ。少し回りくどい表現であるが、要は「標本平均にある程度の幅をもたせてあげる」という考え方だ。そして、この範囲内に確率95％で本当の平均値（母平均）があると推測する。

  • 平均値の95％信頼区間

もちろん、確率95％なので完璧とはいえない。20回に1回くらいは例外もあり得る、というレベルの信頼性である。本来なら確率100％を追求したいところであるが、そうすると「平均値の信頼区間」は無限小～無限大になってしまい、数字としての意味をなさなくなる。そこで、5％くらいは妥協して推測を進めていくのが「95％信頼区間」となる。

なお、医療分野のように信頼性が重視される調査では、「99％信頼区間」が採用されるケースもある。この場合、例外となる確率は1％に低下するが、そのぶん「平均値の信頼区間」は広くなる。

  • 平均値の99％信頼区間

平均値の95％信頼区間の計算方法

それでは、先ほどの例を使って「平均値の95％信頼区間」を求める方法を紹介していこう。「平均値の信頼区間」は、以下の計算式で算出できる。

  • 信頼区間の計算式

「標本平均」と「不偏分散」は前回の連載でも解説しているので、「tの値」がわかれば「平均値の信頼区間」を算出できることになる。

「tの値」はt分布から求められるもので、「自由度」と「信頼区間の確率」に応じて以下の表のように変化する。

  • t分布表

「平均値の信頼区間」を求める場合の「自由度」は、「サンプルデータの個数」から1を引いた値となる。今回の例は10個のデータがあるため、その自由度は10－1＝9となる。よって、信頼区間の確率95％における「tの値」は2.262となる。

では、実際にExcelを使って「平均値の信頼区間」を計算する手順を示していこう。まずは、計算用のセルを以下の図のように用意し、関数AVERAGE()で「標本平均」を求める。

  • 標本平均の算出

今回の例では「標本平均」は81.33という数値になった。続いて、「不偏分散」を求める。前回の連載でも紹介したように、「不偏分散」は関数VAR.S()で算出できる。

  • 不偏分散の算出

今回の例における「不偏分散」は326.79となった。次は「標準誤差」を算出する。先ほど計算式で示したように、「標準誤差」は（不偏分散／データの個数）の平方根で算出できる。よって、関数SQRT()を使って以下のように数式を入力すると、「標準誤差」を求めることができる。

  • 標準誤差の算出

次は、今回の例に該当する「tの値」を求める。Excelには「tの値」を求める関数T.INV.2T()が用意されているため、そのつどt分布表を参照しなくても「tの値」を求めることが可能だ。

関数T.INV.2T()の書式

　＝T.INV.2T(危険率, 自由度)

「危険率」は（1－信頼区間の確率）を示すもので、95％信頼区間の場合は5％（0.05）となる。また、前述したように、「自由度」は（データの個数－1）となる。今回の例は10個のデータがあるため、自由度は9となる。つまり、「=T.INV.2T(0.05,9)」と入力すると、「tの値」を求めることができる。

  • 関数T.INV.2T()で「tの値」を求める

続いては、「tの値」×「標準誤差」を計算して「平均値の誤差」を求める。

  • 平均値の誤差の算出

あとは、この数値を「標本平均」にプラスマイナスするだけだ。これで「平均値の95％信頼区間」を求めることができる。

  • 「信頼区間の最大値」の算出

  • 「信頼区間の最小値」の算出

今回の例では、「平均値の95％信頼区間」＝68.40～94.26（g）、という結果を得ることができた。つまり、68.40～94.26（g）の範囲に95％の確率で「母平均」がある、と考えられる訳だ。

  • 算出された「平均値の95％信頼区間」

この結果を見ることで、ある程度は「標本平均」の信頼性を探ることができる。今回の例における「平均値の95％信頼区間」は68.40～94.26（g）となり、全体で約26gもの幅がある。これでは「信頼性の高い指標」とはいえないであろう。

「標本平均」（81.33）に対する割合で示すと、±15％以上もの誤差があることになる。よって、今回の調査結果をもとに「1袋に詰めるスナック菓子の量」を決定するのは、あまりにも心許ないと考えられる。

このように「平均値の95％信頼区間」を算出すると、サンプル調査から得た平均値（標本平均）の信頼性を検証することが可能となる。

統計学に馴染みのない方は、サンプル調査から得た平均値を「信頼できる数値」と思い込んでしまう傾向があるかもしれない。しかし、必ずしもそうとは限らない。サンプル調査の結果を「統計学的に意味のある数値」とするには、必ず「平均値の95％信頼区間」を確認しておかなければならない。でないと、不十分な調査結果をもとに事業戦略などを立案してしまう恐れがある。

そこで次回は、サンプル調査から得た「標本平均」をより信頼性のある指標にするための対応策を紹介していこう。