今回は、過去の販売実績データをもとに、新たに販売する商品の製作数を決める方法を紹介してみよう。蓄積したデータは、ただ眺めているだけでは意味をなさない。フィルターを使って過去のデータを積極的に活用していくためのヒントとなれば幸いである。
ロスを最小限にするように製作数を決める
今回は、あるTシャツ屋さんが「新しいデザインのTシャツ」を製作する場合を例に、データ分析の手法を紹介していこう。
新しいデザインのTシャツは、以下のような条件で製作する予定である。
・サイズはS、M、Lの3種類
・生地の色は白、黒、緑の3色
・製作数の合計は1,500枚
こういった場合に頭を悩ませるのが、「各サイズ、各色のTシャツをそれぞれ何枚ずつ製作すればよいか?」という問題だ。
勘を頼りに製作数を決めてしまうと、いざ販売を開始したときに「Lサイズは大量に在庫が余っているのに、SサイズとMサイズは売り切れてしまった・・・」といった事態にもなりかねない。これでは、せっかくの販売機会を失ってしまうし、在庫が余っているLサイズのTシャツは製造コストや廃棄コストが無駄になってしまう。
できることなら、消費者のニーズに合わせて製作数を決定したいものである。そこで、過去の販売実績データをもとに製作数を予測する方法を紹介してみよう。
製作数の予測に用いるデータは、これまでに利用してきた表と同じである。この表は、ある期間において、Tシャツの販売数を「デザイン」「色」「サイズ」別にまとめたものとなる。
比例配分を使った製作数の予測
それでは、さっそく手順を解説していこう。まずは、製作数を予測するために以下のような表を用意する。この表は「新しいワークシート」に作成してある。
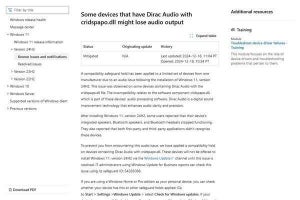
続いて、それぞれのサイズと色について、過去の販売実績を集計していく。たとえば、Sサイズの販売実績を調べたいときは、サイズ「S」の条件でフィルターを実行し、Sサイズだけのデータを抽出する。
本連載の第21回で紹介したように、関数SUBTOTAL()を使って各列の合計を求めている場合は、抽出したデータに応じて計算結果が表示されるようになる。今回の例では、Sサイズの販売実績の合計は5,580枚という結果が表示された。この数値を先ほどの表に書き写す。
同様の手順で、MサイズとLサイズについても過去の販売実績を調べ、その数値を表に書き写す。その後、関数SUM()で合計を算出する。
これで、各サイズ(S/M/L)の販売実績の比率を求められるようになる。この数式は、(各サイズの販売実績)/(合計)となる。オートフィルで数式をコピーできるように、(合計)は絶対参照で指定しておくとよい。
この結果を見ると、Sサイズは約31.7%、Mサイズは約44.2%、Lサイズは約24.1%の比率で売れていることがわかる。よって、新商品も同じ比率で製作すれば、無駄の少ない制作数になると思われる。
色(白/黒/緑)についても過去の販売実績の比率を求めていこう。サイズの抽出条件を解除し、今度は色「白」の抽出条件でフィルターを実行する。今回の例では、色「白」の販売実績の合計は6,734枚という結果が表示された。この数値を先ほどの表に書き写す。
同様の手順で「黒」と「緑」についても過去の販売実績を調べ、その数値を表に書き写す。その後、関数SUM()で合計を算出する。
こちらも(各色の販売実績)/(合計)で比率を算出する。その結果は、「白」が約42.8%、「黒」が約41.3%、「緑」が約15.8%になると判明した。
あとは、サイズと色の比率に合わせて、合計1,500枚になるように各々の製作数を計算していくだけだ。この計算方法を具体的に示すと、合計1,500枚のうち31.7%が「Sサイズ」のTシャツになり、さらにその42.8%が「白」のTシャツになる、と考えられる。これを数式で示すと以下のようになる。
同様の計算を各セルで実行していくと、各々の製作数を求められる。ただし、先ほど示した数式はオートフィルで正しくコピーすることができない。効率よく数式を入力できるように、オートフィルに対応した数式の記述方法も示しておこう。
まず、常に変化しない「製作数」(C2)のセル参照は、絶対参照($C$2)で指定する。続いて、サイズの比率(D5)は、以下のように考えてセル参照を指定する。
・横方向にコピーしたとき ・・・・ 列を変化させない(D列を固定) ・縦方向にコピーしたとき ・・・・ 行を変化させる
よって、D列だけを固定した「$D5」という記述になる。色の比率(E4)は、上記とは逆の考え方になる。4行目だけを固定し、列は変化させるので「E$4」という記述になる。
以上をまとめると、数式の記述は「=$C$2$D5E$4」となる。
このように数式を記述しておくと、オートフィルで縦横にコピーしても、正しい数式を入力できるようになる。
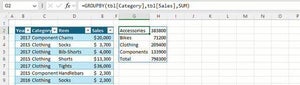
各サイズ、各色の計算結果は、以下の図のようになる。
この結果を見ると、「Sサイズ、白」のTシャツは約204枚、「Mサイズ、白」のTシャツは約284枚、「Lサイズ、白」のTシャツは約155枚、・・・と製作数を決めていけばよいことになる。この計算結果には小数点以下の数値が含まれているので、これらの値をそのまま採用する訳にはいかないが、製作数を決める際の目安としては十分に役立つ分析結果といえるだろう。
この手法を利用するときの注意点
このように、過去のデータをもとに、新たに販売する商品の製作数を予測することも可能である。ただし、先ほど示した製作数の予測には、大きな間違いがあることも述べておかなければならない。
まずは、サイズについて。こちらは過去の販売実績が十分に参考になると思われる。前回に「Sサイズ」を購入した顧客は、次回も「Sサイズ」を購入すると考えられるので、新商品においてもS:M:Lの比率は大きく変わらないと予測される。よって、こちらは信頼に足りるデータといえる。
一方、「色」についてはどうかというと、前回に「白」のTシャツを購入した顧客が次回も「白」のTシャツを購入するとは限らない。「どの色が人気を集めるか?」は、Tシャツのデザインや流行にも左右されるため、過去のデータをそのまま信頼するのは危険だ。よって、かなりの不確定要素を含むデータとして捉えておく必要がある。
さらに、「色」のデータは統計学的に間違った処理が行われていることも認識しておかなければならない。というのも、過去の販売実績データにおいて、「S、M、Lのサイズ」はすべてのデザインにラインアップされているが、「色」はどのデザインにも共通するラインアップではないからだ。
「白」や「黒」といった色は、ほとんどのTシャツ(デザイン)にラインアップされているが、「緑」がラインアップされているTシャツ(デザイン)は数種類しかない。にもかかわらず同じ条件で集計すると、販売実績の合計は「白」と「黒」が多く、「緑」は少ない、という結果になるのは当然である。
より正確に予測するには、「白、黒、緑がラインアップされているデザイン」についてのみ、販売実績の合計を比較すべきである。ただし、この場合はデータ数が少なすぎて十分な結果を得られない可能性もある。
要するに、「サイズ」の比率は信頼できるが、「色」の比率は信頼性に欠ける、ということだ。今回、紹介した手法はあくまで計算上での話であり、結果をそのまま採用できるかどうかはケース by ケースとなる。算出された数値を参考に、最終的には、担当者が勘と経験を頼りに製作数を決めていく、というのが実際の活用方法になるだろう。
十分なビッグデータがあり、流行や好みも予測可能なAIがある、という時代が来れば、「色」についても信頼性の高い予測ができるようになるかもしれない。しかし、それはもう少し未来の話になりそうだ。仮にそういう時代が来たとしても、AIを使いこなすには多少の経験が求められるし、利用料が高くてAIを使えるほどの余裕がない、というケースも十分にありえる。そう考えると、今回紹介した手法は、まだまだ利用価値のある手法といえるだろう。