今回は、関数RANK()を使ってランキングを求める方法を紹介してみよう。「並べ替え」だけではスムーズにランキングを作成できない場合に活用するとよいだろう。さらに、各項目のランキングから総合順位(総合ランキング)を算出するときの応用的な使い方も紹介する。
前回の連載で紹介した手法の問題点
前回の連載では、各項目についてランキングを求め、それをもとに総合ランキングを算出する方法を紹介した。しかし、この方法には1つだけ弱点がある。それは「1位タイ」や「2位タイ」などの同順位のランキングが出現した場合に対応が面倒になることだ。
今回も「歓送迎会のお店選び」を例に詳しく解説していこう。ビジネス感に欠ける例で申し訳ないが、「誰もが理解しやすい事例」として参考にしていただきたい。
以下の図は、前回の表に「時間」のデータを追加したものとなる。ここでいう「時間」とは「飲み放題の時間」を指している。もちろん、飲み放題の時間が長いほど「良い店」になると考えられる。
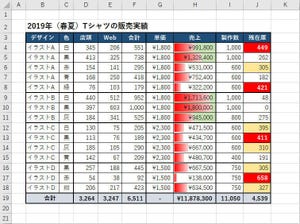
前回の連載と同様の手順で「時間」についても大きい順に並べ替えてランキングを作成すると、以下の図のような結果になる。
「150分」のデータが1位になるのは当然として、それ以降のデータは同じ「120分」であるにも関わらず、2位、3位、4位という結果になってしまう。5~8位も同様で、同じ「90分」というデータなのにランキングに差がついてしまっている。これでは正しい総合ランキングを算出することは不可能だ。
「並べ替え」→「オートフィルで連番をコピー」という手順で作業を行った場合、このようなミスが生じてしまう恐れがある。データを確認しながら、手作業で1、2、3、・・・とランキングを付けていけば回避できる問題ではあるが、これは少し面倒な作業といえるだろう。
関数RANK()の使い方
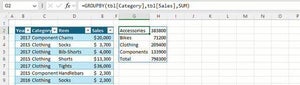
このような場合に活用できるのが関数RANK()である。関数RANK()は、指定したセル範囲内で「その数値が何番目にあるか?」を返してくれる関数で、先ほど示した例のように「同順位のデータ」が複数ある場合にも対応できるのが利点となる。
関数RANK()を使用するには、以下の3つの引数が必要となる。
■関数RANK()の書式
=RANK(数値, 参照するセル範囲, 順序)
先ほど紹介した「時間」のランキングを求める場合を例に、関数RANK()の入力手順を詳しく解説していこう。
まずは、第1引数に「ランキングを求める数値」を指定する。今回の例の場合、「時間」のデータが入力されている「F5」を指定すればよい。
続いて、「母集団となるデータのセル範囲」を第2引数に指定する。今回の例では「F5~F12の中で何番目か?」を求めたいので「F5:F12」と入力する。ただし、普通に相対参照でセル範囲を指定してしまうと、オートフィルで関数RANK()をしたときに、母集団となるセル範囲まで自動補正されてしまう。このセル範囲を自動補正しないようにするには、セル範囲を絶対参照で指定しておく必要がある。
いちいち「$」を入力するのが面倒な場合は、「F5:F12」と入力したあと(またはドラッグによりセル範囲を指定したあと)、「F4」キーで絶対参照に変換すると入力の手間を省けるだろう。
最後に、ランキングを求める「順序」を指定する。最も大きい数値を1位(降順)にしたい場合は0(ゼロ)、最も小さい数値を1位(昇順)にしたい場合は1を指定すればよい。今回の例では「時間」の数値が大きくなるほど上位にしたいので0(降順)を指定した。最後に「カッコ閉じ」を忘れずに記入すると、関数RANK()の入力は完了となる。
あとは、関数RANK()をオートフィルでコピーするだけ。第2引数のセル範囲を絶対参照で指定していれば、全データのランキングを正しく求めることができる。
この結果を見ると、「120分」のデータはすべて2位、「90分」のデータはすべて5位になっているのが確認できる。つまり、「同じデータ」を「同じ順位」に変換できたことになる。
総合順位の算出
念のため、「評判」「価格」「距離」「時間」の4項目について総合順位を算出する方法も紹介しておこう。といっても、この手順は前回の連載と同じである。ここでは関数SUM()により各ランキングを「足し算」して総合ポイントを算出した。
あとは「総合ポイント」の小さい順にデータを並べ替えるだけ。なお、この「総合ポイント」も同じ数値になるデータがいくつか見受けられる。よって、総合順位をわかりやすく示したい場合にも関数RANK()が活用できる。
今回は「総合ポイント」の小さい順に総合順位を求めるので、関数RANK()の第3引数には1(昇順)を指定すればよい。
参考までに総合順位を紹介しておくと、「舞那比飯店」と「間井那弥蕎麦」の2店舗が1位タイ、「Ristorante Mynavi」が3位という結果になった。
関数RANK()を使う場合は「並べ替え」が不要
これまでに紹介してきた手法では、「並べ替え」により各項目のランキングを求めていた。しかし、関数RANK()を使う場合は、この「並べ替え」も不要となる。数値の並び順がバラバラであっても正しいランキングを求めることが可能だ。
関数RANK()の記述方法は同じなので、詳しい解説は省略して、画像だけで紹介しておこう。関数RANK()を使うメリットの一つとして覚えておくとよいだろう。
各項目の比重を変化させたランキング
関数RANK()を使った手法は、それぞれの項目の重要度を変化させる場合にも応用できる。これまでに紹介した例では、「評判」「価格」「距離」「時間」の4項目を同じ比重で扱ってきたが、「特定の項目だけ比重を大きくしたい」と考える場合もあるだろう。
たとえば、「やっぱり評判(味)を重視したい」という場合は、「評判」のランキングに適当な数値を「掛け算」してあげればよい。以下の例では「評判」のランキングを2倍にしているため、「評判」のランキングが「価格」「距離」「時間」よりも2倍の比重で評価されることになる。
もちろん、「評判」のランキング(数値)が変化すれば、それに応じて「総合ポイント」や「総合順位」の数値も変化する。今回の結果を総合順位の小さい順に並べ替えると、総合1位は「間井那弥蕎麦」、総合2位は「舞那比飯店」、総合3位は「肉バル MYNAVI」と「Trattoria Mynavi」の2店舗、という結果に変化していることを確認できる。
このように関数RANK()を使ってランキングを求めると、各項目の比重を手軽に変更できるようになる。各項目のランキングを1、2、3、・・・と入力する場合に比べて「より自由度が高くなった」といえるだろう。複数の項目から総合ランキングを算出する手法の一つとして覚えておくとよい。