パラメトリックモーション
(動画中の)2枚のフレーム間での動きを推定する問題において、動画中の2枚の画像のうち、前フレーム(これを「画像1」とします)を動き分だけ変形させて後フレーム(これを「画像2」とします)に位置合わせを行いたい時に、思いつく一番単純な動きのモデルは「画像1が画像2に向けて、水平方向にu、垂直方向にvだけ平行移動した」というものです。
例えば、パノラマ写真を撮影するために、カメラが綺麗に水平方向に平行移動したと仮定できる撮影が行えた場合、2つの画像間で重複している領域では、全ての画素において各画素が値uだけ平行移動して画像2の状態に移ったと見なすことができます。
しかし、今議論している「2フレーム間の動き推定」をはじめとした画像間の位置合わせ(レジストレーション)問題の多くは、平行移動モデルだけでは当然ながら画像間の動きの表現モデルが十分ではありません。例えば、すでに本連載で紹介した「スティッチング」では、ホモグラフィなどの複雑な変換を、カメラ間の動きモデルとして仮定する必要がありました。平行移動モデルでは全画素を同じ値(u,v)だけ動かせば済むのですが、ホモグラフィが動きモデルの場合は、各画素で移動量がそれぞれ違った値に変わってきます。画像中の全画素がどれだけ移動したかの移動ベクトルと各画素に求めても良いのですが、せっかく「全体としては1つの動きモデルで移動した」と仮定しているのですから、もう少しコンパクトな方法がありそうです。そもそも、このままだと画像1の各画素に対して、移動先の画素を画像2から個別に探索しないといけなくなってしまい、このままでは非常に非効率的な動き推定の計算アルゴリズムとなってしまいます。
そこで、特定の領域中の各画素が「ある特定の1つの動き表現(平行移動やアフィン変換、ホモグラフィなど)」に沿って統一的に移動したとみなし、その動き表現のパラメータを変えると、対象領域の場所全体がそのパラメータの値にそった動きモデルにより、統一的に移動されるという表現を導入します。これを「パラメトリックモーション」による動き表現と呼びます。
パラメトリックモーションを用いると、画像2中の各点の座標値を動きパラメータと画像1の点の座標を用いて「パラメトリックに」表すことができ、さきほどあげた「非効率な動きベクトル計算」も回避できる、コンパクトな動き表現が手に入るのです(平行移動自身もパラメトリックモーションの1種であることには注意)。
パラメトリックモーションを用いると、画像1、画像2の間で「画素の値が一番似ている画素同士の対応」を探索さえできれば、その対応点ペアを用いれば自分が仮定したパラメトリックモーションのモデルのパラメータ値(すなわちその動きモデルの移動量)を推定することができます(実際のパラメータ値の推定の方法は、このあとオプティカルフローの仕組みの説明を通して紹介していくことにします)。
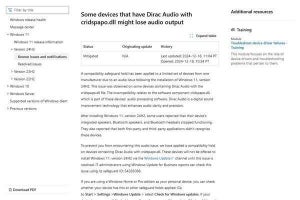
パラメトリックモーションは、以下の図に示すような各種の画像変換を動きのモデルとして用います。
図中上部の(画像)座標系上で、一番左の濃い青色の正方形が、移動前の画像変換される前の状態を示しています。それ以外が各モデルによる変換での「移動されたあとの状態」を示しています。
これらの動きモデルは「画像変換」と呼んだくらいで、どの動きモデルも(画像の中での)2次元的な変換を表現したものです。このうち「並進」は縦と横に平行移動するモデルです。「相似変換」は「回転+並進+スケーリング(拡大縮小)」のモデル、アフィン変換は、移動前の矩形が平行な線同士は平行なまま平行四辺形に変換できるモデルで、射影変換(ホモグラフィ)は4つの頂点が任意に別の移動量で動けるモデルです。
繰り返しになりますが、画像間の動きにパラメトリックモーションを用いると、動きモデルにより移動後の各点を数少ないパラメータで表現でき、動き推定の計算も楽になり、計算コストも下がります。一方で、動画中に同時に独立して起こる各動きをすべて推定するには、パラメトリックモーションだけだと厳しくなります。もちろん、小さな領域ごとにパラメトリックモーションのいずれかのモデルによる移動が成立している画像中の領域は、個別に独立したパラメトリックモーションを想定して動き推定を行うことはできます。しかし、自然界を撮影した動画中には、そもそもパラメトリックモーションでは表現できない動きがたくさん存在します。つまり、さきほど紹介した「並進、回転、フィン変換、ホモグラフィ」だけでは、これらの動きモデルの以外の歪みや移動、変形などが表現しきれないわけです。そこで、そうした動画の動きを推定するには、「オプティカルフロー」という動き表現と、その推定方法が必要となってきます。