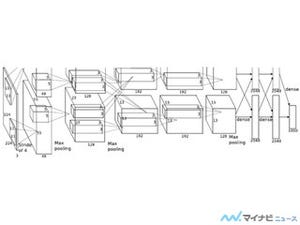
ディープラーニングの学習

しかし、精度の高い推論を行うためには、各ニューロンの入力の重みを適切な値に設定する必要がある。現在はより複雑なネットが開発されており、AlexNetは規模が小さいのであるが、それでも、65万個のニューロンを使っており、約6000万個の入力の重みの値を決めなければならない。これを決めるのが「学習(Learning)」である。

1変数のニュートンラプソン法では、y=f(x)の微分係数のdy/dxを計算し、xを調整してy=0になるようにしていくが、CNN(Convolutional Neural Network)の場合は変数(重み)の数が膨大であるので、Stochastic Gradient Descent(SGD)というアルゴリズムが使われる。

それぞれの重みに対する認識結果の誤差(学習の場合は、ロスと呼ばれる)の偏微分を計算し、その勾配が大きい方に重みを調整していく。ニュートンラプソン法でもそうであるが、1回の修正でロスがゼロになるように修正するのは過激で、補正しすぎて振動するなどしてしまい、上手くいかないので、通常、SGDでは、計算された値の1/1000とか1/10000の補正を行なう。そして、収束に近づくとこの比率をさらに小さくしていく。

ネットワークにもよるが、この調整を数10回から100回程度繰り返して、重みの値を収束させる。ILSVRC 2012の場合、AlexNetでは120,000画像を使って学習している。NVIDIAのGTX580 GPU(単精度のピーク演算性能は約1.58TFlops)を2個使い、この学習には5～6日を要している。

調整のループ回数を80回とすると、12,000画像の学習には、100万回の推論が必要となる。

入力重みの変化でロスがどう変化するかを求める

出力層の各出力が、各入力の変化でどう変わるかは、で表わされる。出力Yがn個あり、入力Xがm個あると、この値はn×mの行列になる。各出力が、各入力の重みの変化でどう変わるかはで表わされ、これもn×mの行列になる。

しかし、Yは、Yi= W1*X1+W2*X2+W3*X3、…のような1次式であるので、はWjであるし、はXjであるので計算は簡単である。そして、ReLUが付いている場合も出力が正であればそのまま、負であればゼロにすればよいので、これも簡単である。

問題は、前段の重みや入力の変化に対する最終出力の変化をどうやって求めるかである。そのやり方であるが、出力層をn層目とすると、その前のn-1層の出力が、n-1層の各入力や入力の重みの変化でどう影響を受けるかを求める。このやり方は、出力層の場合と同じである。

そして、図9-3に示すように、出力層nの最終出力の入力変化に対する偏微分の行列に、n-1層の出力のn-1層の入力の変化に対する偏微分の行列を掛ければ、最終出力に対するn-1層の入力の変化に対する偏微分が得られる。

ただし、n-1層の出力は、n層の複数のニューロンに繋がっているので、その接続に従って、1つの出力を複製してやる必要がある。

そして、この作業を入力層に到達するまで繰り返せば、すべての入力と重みに対する偏微分が求まる。この作業をBackward Propagationと言う。

図9-3 前段の入力や入力の重みが、最終出力にどう影響するかを求めるやり方

この説明から分かるように、大量の計算が必要となるのは、図9-3に示したパスに従って、各層の出力の入力と重みの変化に対する偏微分の行列を掛けて行くBackpropagationの作業である。つまり、学習も計算という点では、行列の乗算を繰り返すことになる。

そして、各層の入力の重みによる偏微分が求まると、この値に通常ηと書かれる小さな値を掛けて全ての入力の重みを更新する。ただし、ロスは非線形な関数であるので、一度でロスをゼロにすることはできず、この作業を繰り返してロスをゼロに近づける。