10進数の演算ハードウェア

ExponentとBias

Exponentはdecimal32では6ビット、decimal64では8ビット、decimal128では12ビットのフィールドを持ち、こちらは10進数ではなく、2進数で表現される。ビット数が少ないので、入出力に当たって2進10進変換するオーバヘッドは大きくなく、一方、Exponentが2進数であれば、従来の2進浮動小数点演算器と指数部の処理回路を共通化できるというメリットがあるという理由である。

表現できる最大の数値が、例えば10の99乗であったとすると、最小の数値は10の-99乗というのがバランスが良い。このようにすれば、逆数をとってもオーバーフローやアンダーフローすることが無く、2進の浮動小数点形式はこの要件を満たしている。しかし、10進形式のCoefficientは整数で小数点は右端にあるので、2進形式のようにExponentの正、負の値が絶対値で同じであると、Coefficientの桁数分、最大値の方が大きくなってしまう。このため、BiasはExponentの最大値の半分より少し上側にずれており、decimal32では101、decimal64では398、decimal128では6176と定められている。decimal32のExponentが6ビットなら最大値は63なのに、何故、Biasが101になるのかという疑問を持たれた読者は、まじめに読んでいただいている貴重な読者で、その理由は次項のCombination Fieldの説明を読んで戴きたい。

Combination Field

10ビットの整数倍のCoefficient部と、実用上、適当な長さのExponent部と符号1ビットを取ると、5ビット程度が残る。10ビットには足りないので精度を10進3桁増やすことはできないし、さりとて、Exponent部をやたらに長くしても無駄が多い。ということで、頭をひねってCombination Fieldと呼ぶ5ビットのフィールドを作った。

Combination Fieldは、その名の通り、ExponentとCoefficientの両方のビット数を補うものであり、さらに、無限大やNaNなどを記述する機能を持っている。

Combination Field 5ビット	タイプ	Exponent MSB 2ビット	Coefficient MSD 4ビット
a b c d e	数値	a b	0 c d e
1 1 c d e	数値	c d	1 0 0 e
1 1 1 1 0	∞	- -	- - - -
1 1 1 1 1	NaN	- -	- - - -

この表に見られるように、Combination Fieldは、Exponentの最上位の2ビットとCoefficientの最上位の10進1桁を拡張している。但し、この表の第一行のabや第二行のcdは、"11"以外の値でなければならないので、数値的にはExponentの拡張はフル2ビットの0～3ではなく、0～2にしか拡張できない。そして、10進1桁は9までの数値しかないことを利用して、空き領域に無限大とNaNを定義している。

これらのCombination fieldの値がExponentやCoefficientの最上位になることから、ExponentやCoefficientを表わす本体のフィールドは継続する下位ビットやディジットという位置づけになり、Exponent ContinuationとかCoefficient Continuationという名前になっている。

このような拡張があるので、decimal32のExponentは0～63ではなく0～191となり、Biasを101とすることにより、10の-101乗から+90乗までの指数を表わすことができるようになっている。

10進浮動小数点データの範囲

以上、述べたようなコーディングにより、それぞれのデータ形式で表現できる数値の範囲を以下の表にまとめる。

	decimal32	decimal64	decimal128
総ビット長	32	64	128
有効10進桁数	7	16	34
Exponentの最大値	191	767	12287
Exponentのバイアス	101	398	6176
指数の最小値	-101	-398	-6176
指数の最大値	90	369	6111

10進数の演算ハードウェア

4ビットのうちの0～9までの数値を使うBCD形式のデータの足し算は、両者が普通の2進数と思って加算を行い、

• 各桁の合計が9以下:そのまま
• 合計が10以上となった桁:更に+6

というステップで行えば良い。例えば、合計が12になった桁に+6すると18となり、2進4ビットのアダーの出力は2となり、更に、上位の桁へのキャリーが生成されるので、正しいBCD形式の結果が得られる。そして、引き算の場合には、各桁の値が負になった場合は、上の桁を-1して、その桁に10を足し込めば良い。

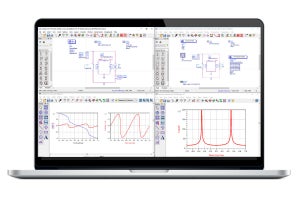
図29にIBMのPOWER6プロセサの10進浮動小数点演算ユニットの構成を示す。ユニットとしては四則演算と各種コンバージョンをサポートしているが、ハードウェアとしては、DPDとBCDの変換回路とBCDの加算器、そして掛け算のための2倍と5倍の値の生成回路と必要なレジスタといった軽い構成で、スライドにも、ハードウェアとしては最小限の実装であると断っている。

しかし、このような比較的簡単な実装でも、Javaの10進浮動小数点演算を使う実アプリで7倍以上、C#では4倍の性能が得られたという。

演算器シリーズの終わりにあたって

当コラムの70回から長々と続いてきた演算器シリーズはこれで終わりである。かねてより、演算器についてまとめて書いてみたいと思っていたのであるが、このような機会を与えて戴いたマイコミジャーナル編集部に深く感謝する次第である。また、ヘネパタ本(David A. Patterson & John L. Hennessy著 Computer Architecture: A Quantitative Approach)には演算器についてAppendixに書いてあった(この部分の著者はXeroxのGoldberg氏である)が、3版以降では無くなってしまった。その他のコンピュータの教科書などでも、演算器に関してこれほど網羅的、かつ、詳しく書いたものは筆者の知る範囲では存在せず、読者のお役に立てるのではないかと思う。