計算量が多くて難しいとされる物質の結晶構造探索について、無機化合物で計算コスト少なく網羅的に探索する手法を東京大学物性研究所の尾崎泰助教授(計算物質科学)らが開発した。経験則を不等式で表して「これ以上はダメ」といった拘束条件とするのがミソ。原子の配置と化学結合の最適化を繰り返して最適解を求める。酸化物や硫化物に特化した手法だが、将来的にはイオン結合性結晶の構造探索にも応用が進む可能性もあり、2024年ノーベル化学賞「タンパク質の構造予測」のように新材料の発見に役立つと見込まれる。
無機化合物は概ね原子が周期的に並んだ結晶構造を取る。物質を構成する原子によってどんな結晶構造を取るのか探索する時は、電子のふるまいを量子力学の基礎方程式から厳密に計算することで物質の安定構造や物性を予測する「第一原理計算」を用いるのが主流だ。
しかし、取り得る形や原子の配置全てを考慮して結晶構造の安定性をエネルギー的に評価しながら、可能性のある構造を探索すると膨大な計算量となる。第一原理計算の研究をする尾崎教授によると、世界上位の計算速度を誇る理化学研究所のスーパーコンピューター「富岳」で数十万の構造を試行するといったレベルの計算コストがかかるという。
一方、無機化合物の結晶構造を考察する時には、実験などで現実的に取り得る構造について研究者が経験則的な知見を持っている。尾崎教授の下で大学院生として研究していた産業技術総合研究所の小正路(こしょうじ)崚太郎研究員(計算物質科学)は、「だいたいこれくらいまで」「これ以上は影響しない」といった知見を、ビジネスやエンジニアリングの分野で合理的意思決定を支援するのに用いられることがある「数理計画問題」に取り入れれば、計算で結晶構造を探索できると考えた。「拘束条件」で条件を満たすものを絞り込むやり方で全ての候補を計算せずにすむため、計算コストを減らせるという。
拘束条件としたのは「最密球充填構造」「化学結合」「配位多面体」「多面体の連結」の4つ。最も重要なのが「最密球充填構造」で、陰イオン(アニオン)が最も密になる最小距離をとるような不等式条件とした。「化学結合」についてはアニオンと金属の陽イオン(カチオン)のあるべき距離を不等式条件で表した。「配位多面体」はカチオンと結びつくアニオン数を等式で表した。「多面体の連結」は多面体が結びつく時に、点か辺、面のどこでくっつくかで強さが異なることを不等式で表した。
結晶構造の探索では、カチオンが取り得る大きさごとに11個を想定した「モデルカチオン」を、物質を構成する元素ごとに対応させる。原子番号が近く似ている元素ごとに微妙に異なるパラメーターで計算するより、大きさや形は概ね同じになるモデルカチオンで計算した方が効率的で、結晶構造探索の手間が省ける。
開発した探索法で、2価のアニオンである酸素イオンと、酸素イオンと同じ大きさのカチオンA、八面体のカチオンBを3:1:1の比率で混ぜたとして、パソコンで計算してみると、20分余りで4つの解が見つかった。4つともペロブスカイト構造など実験的に知られた結晶構造であり、最適解を得ているらしいと判断できた。他にも、超伝導体となる銅酸化物の構造や、構成部分にイオン結合のような柔らかい結合が見られるアルファ(α)パイロクロア構造を再現することもできたという。
-
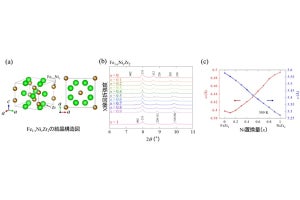
決まった数の酸素イオン(黄色の丸)が接するカチオンを混合して求めた結晶構造の最適解の例。左は銅酸化物超伝導体。右は青い部分に柔らかい結合があるαパイロクロア構造体(産業技術総合研究所の小正路崚太郎研究員提供)
数理計画問題に基づく結晶構造探索法は、最適解の候補を絞りこむことで計算コストを抑えているが、最後は第一原理計算を用いて最適解を出す。小正路研究員は「計算コストを少なく網羅的探索をすることで意外な結晶構造を見つける機会が増えれば、材料探索からデバイス応用までの研究プロセスを加速できる」と話す。
研究は米物理学会の科学誌「フィジカル レビュー マテリアルズ」電子版に11月6日付けで掲載された。
|
関連記事 |