九大、メビウスの輪を採用して初の1次元自由度の劣決定リンク機構を創成

九州大学(九大)は4月24日、6つの合同な四面体が数珠つなぎに輪をなして連なった折り紙である「カライドサイクル」の構造を数学的に解析し、環状のリンク機構を離散的な曲線として定式化することにより、メビウスの輪と同じつながり方を持つ「メビウス・カライドサイクル」の構成に成功したことを発表した。

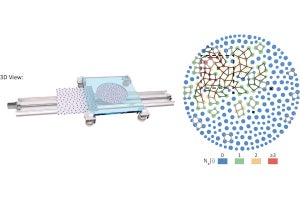
• (左)12個のねじれたパネル。(右)9個の四面体から構成されたメビウス・カライドサイクル。メビウス・カライドサイクルの動きの本質は、隣り合うヒンジの位置関係だけで決まるので、パネルや四面体である必要はなく、キャラクターなどで作っても良い。数学的な条件さえ満たせばその特別な性質が保証される、適用範囲の広い法則である。細長い紙の両端を540度ひねって貼り合わせることでできる表裏のない帯・メビウスの輪の形をしていることがわかる(出所:九大プレスリリースPDF)

同成果は、九大 マス・フォア・インダストリ研究所の鍛冶静雄教授らの研究チームによるもの。詳細は、非線形システムとその数学的構造を扱う学術誌「Nonlinear Systems and Their Remarkable Mathematical Structures」に掲載された。

カライドサイクルという折り紙は、6つの合同な四面体が数珠つなぎに輪をなして連なったもので、クルクルと無限に回すことができることが特徴だ。パンタグラフやワイパー、折り畳み機構などと同じく、リンク機構と呼ばれるものの一種だ。

こうした生活の中で活用されているリンク機構だが、その研究において、特に「劣決定」と呼ばれる性質を持つ機構は解析が難しいとされる。これまでその劣決定において、1次元自由度の動きを持つ本質的な機構は知られていなかった。カライドサイクルに関しても、四面体の個数を増やすことはできるが、増えるにつれてたわみやすく動きが不安定になり、うまく回せなくなってしまっていた。そこで研究チームは今回、カライドサイクルの構造について数学的に解析を進めたという。

解析の結果、環状のリンク機構を離散的な曲線として定式化することにより、1次元自由度を持つ初の劣決定リンク機構であることを確認。四面体が7つ以上の場合でも、特別に計算された四面体を使うことで、たわむことなく綺麗に回ることを実証した。そして、メビウスの輪のように裏表のないつながり方をしていることから、「メビウス・カライドサイクル」と命名された。

メビウス・カライドサイクルの特性は、一定の角度でねじれながらヒンジ(蝶番)によって連なった機構が等しく持つ幾何的性質であり、材質にもヒンジ間をつなぐ剛体の形状にも依存しない。さらに、回転時に弾性エネルギーが一定であること、角運動量を与えることなく向きを変えられることなどの性質も有する。

この特性は、目に見える大きさであればスクリューや攪拌機に、ミクロの世界では高分子領域へ、大きなものでは宇宙アンテナなど、さまざまなスケールでの応用の可能性を持つという。なお、メビウス・カライドサイクルは折り紙で作成することもでき、参考資料として折り紙の設計図や3Dプリント可能なデータが公開されている。

また、メビウス・カライドサイクルは応用上の有用性だけでなく、数学的対象としても重要であることもわかってきたという。その動きは、物理に起源を持つ可積分系と呼ばれる特別な微分方程式で記述される一方、頂点の座標は連立二次方程式で表される実代数多様体という図形になっている。帯としてのねじれの数や自分自身との絡まり方は結び目理論を用いて記述される。このようにメビウス・カライドサイクルは、現代数学のいくつもの分野をつなぐ交差点の役割を果たすと同時に、それら抽象的な数学概念が、手で触れることのできる形で具現化した稀有な存在でもあるとしている。そして今後、折り紙で作れるカライドサイクルの研究を通して、新たな数学が生まれることが期待されるとした。