京大など、正負の電荷の粒子間で斥力が働く状況を作り出すことに成功

京都大学(京大)と理化学研究所(理研)は2月28日、「シュウィンガー模型」と呼ばれる1次元量子系において、電荷が反対の粒子間に通常とは逆の斥力が働く状況を、数値シミュレーションにより実現することに成功したと発表した。

同成果は、京大基礎物理学研究所の本多正純助教、同・谷崎佑弥助教、理研の伊藤悦子協力研究員、米・ブルックヘブン国立研究所の菊池勇太研究員(現・Cambridge Quantum Computing Japan研究員)らの国際共同研究チームによるもの。詳細は、日本物理学会が刊行する理論物理と実験物理を扱う欧文オープンアクセスジャーナル「Progress of Theoretical and Experimental Physics」に掲載された。

自然界の4つの力の1つである電磁気力は、電気的なものと磁気的なものに分けられ、電気的な力は電荷を持った粒子の間で作用する。電荷は通常、正負が同じ粒子の間には斥力が、正負が反対の粒子の間には引力が働くとされているが、近年、空間が1次元の低次元系であるシュウィンガー模型においてはその常識が成り立たず、正負が反対の粒子の間に斥力が働くことが予言されていた。

シュウィンガー模型は、基本的な粒子として光子と電荷を持つ粒子が結合した1次元量子系と想定されており、互いに反対の電荷を持つ2つの重い粒子(プローブ電荷)の間に働く力を考えると、その定性的な振る舞いが模型のパラメータの値に依存して3つのパターンに分かれることが指摘されていた。そのうち2つは、さまざまな状況で起きることが知られている現象だが、残りの1つは「斥力が働く。特に、勝手に伸びるようなひも(負の張力を持つ)でつながれているかのような力が働く」という通常では起こらない特殊な現象であり、まだほとんど研究がされていない状況であるという。

また、この現象が起こると予言されていた模型のパラメータ領域は、これまでの素粒子理論分野における標準的な数値計算の手法(マルコフ連鎖モンテカルロ法)では、「符号問題」により、必要な計算量が莫大になり、数値シミュレーションが困難とされていた。そこで研究チームは今回、モンテカルロ法とは別の手法として、ゲート型量子計算機を使用する際に用いられる量子アルゴリズムの一種である「断熱的状態準備法」を用いることにしたという。

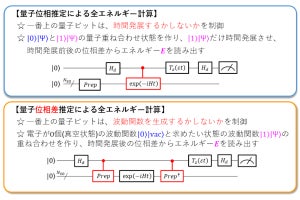
具体的な手順としては、シュウィンガー模型が置かれている1次元の連続的な空間を格子に切り、数学的に等価なスピン系に変換することで、模型を量子アルゴリズムが直接適用できる形に置換。そこに断熱的状態準備法を適用し、プローブ電荷が置かれている状況での模型の様子を調べるというもので、プローブ電荷の間に斥力が働くと指摘されている状況を数値シミュレーションで直接調べることをできるようにしたとする。

実際に、IBMの量子計算機用の古典シミュレータを用いてプローブ電荷間の力が計算されたところ、あるパラメータ領域においては実際に斥力が働くことが判明したという。

この成果について研究チームでは、通常の方法では解析が難しい状況において、量子アルゴリズムによる新たな手法を用いて新奇な現象を直接調べることができたことに意義があるとしているほか、この成功を受けて今後は、同じく符号問題により通常の方法では数値シミュレーションが難しいといわれている、初期宇宙の時間発展や有限密度領域における初期宇宙の相構造などの重要な問題が、今回のような量子アルゴリズムを用いたアプローチで明らかになっていくことが期待されるともしている。