岐阜大、微粒子のエネルギーと振動数が極小となる「魔法数」の存在を確認

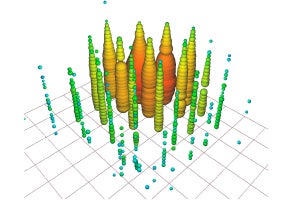
岐阜大学は9月21日、球面上の荷電粒子系を微粒子とみなし、その固有振動数の解析を行うことにより、微粒子のエネルギーだけでなく振動数も極小となるような「魔法数(マジックナンバー)」が存在することを明らかにしたと発表した。

同成果は、岐阜大工学部応用物理コースの小野頌太助教によるもの。詳細は、米物理学会が刊行する物性と物質に関する学術誌「Physical Review B」に掲載された。

数十個から数百個の原子が凝集したナノスケールの微粒子(少数原子系、クラスターなどとも呼ばれる分子)は、ある特定の個数の原子が集まって合成されることが知られている。その特定の個数は「魔法数」と呼ばれている(原子核が安定する陽子と中性子の特定の個数についても魔法数という言葉が使われているが、今回は分子中における原子数のことを指す)。

ある特定の個数の原子数で分子が安定するのは、魔法数の微粒子は幾何学的に高い対称性を持ち、そのエネルギーが低く安定であり、それゆえに合成されやすいことが理由と理解されている。

そうした魔法数の決定を数学的に考えると、エネルギーは原子の座標の関数で表すことが可能だという。微粒子を構成する原子の座標を決めると、その微粒子のエネルギーが1つ決定され、原子の座標を変化させるとエネルギーも変化するため、エネルギーは曲面を描き、そうしてできた山や谷の中で、深い谷の底が安定な微粒子構造に相当するという。

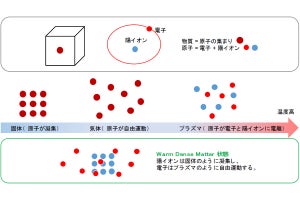
魔法数を決定するためのエネルギーvs原子数の関係。原子数M1およびM2のエネルギーは、それぞれ原子数がM1±1、M2±1の場合よりも小さい。一般に、魔法数を持つ微粒子は、正十二面体構造などの幾何学的に高い対称性を持つという (出所:岐阜大プレスリリースPDF)

これまで、微粒子の「谷の深さ」に関する研究は数多く行われてきたが、「谷の形状」に注目する研究はほぼ皆無だったという。微粒子の固有振動数は谷の形状によって決まるため、その詳細を理解することはナノサイエンスにおける重要な問題とする。

そこで今回の研究では、「球面上の荷電粒子系」を微粒子とみなし、そのエネルギーと最大振動数を粒子数Nの関数として計算することにしたという。

その結果、エネルギーが極小となるNでは、いくつかの例外を除き、最大振動数も極小となることが判明。これは「深い谷の底は滑らかである」ということを示唆しているという。

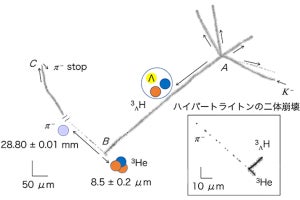
(左)球面上の荷電粒子系における魔法数を決定するグラフ。N=12、32、72、132、192の場合、エネルギーと最大振動数が同時に極小となる(発表論文のFigure2より引用されたグラフ)。(右)エネルギーの深い谷底は滑らかであるということの概念図。この場合、底にあるボールはゆっくりと振動するという (出所:岐阜大プレスリリースPDF)