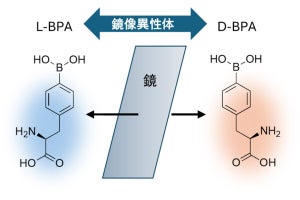
中部大学、北海道大学(北大)、名古屋大学(名大)、オーストリア・ウィーン工科大学、インターネット総合研究所の5者は6月25日、中性子のスピンを測定する実験により、「小澤の不等式」で知られる小澤特任教授(中部大/名大)が2019年に考案した、ミクロな物体の測定誤差を正確に定めるための新しい理論を検証することに成功したと発表した。
同成果は、中部大学AI数理データサイエンスセンターの小澤正直特任教授(名大名誉教授兼同・大学院情報学研究科 招へい教員)、北大大学院 工学研究院の長谷川祐司教授(ウィーン工科大 准教授)らの国際共同研究チームによるもの。詳細は、英科学誌「Nature」系の「npj Quantum Information」にオンライン掲載された。
素粒子を扱うミクロスケールの世界は、そのミクロスケールの物理を扱う量子力学の根幹に位置するハイゼンベルクの「不確定性原理」のように、マクロスケールの世界とは異なる法則が存在していることが知られている。
素粒子は、その位置と運動量の両方を同時に正確に(誤差ゼロで)測定することができず、必ず本来の値との誤差が生じるとされている。そのため、量子現象の理解には、測定の誤差を正確に捉えることが必要とされてきた。
しかし、量子物理学において測定誤差の概念を定義することは、難しい問題とされており、とりわけ小澤特任教授が2003年に提唱した「小澤の不等式」に代表される、不確定性原理を現代的に再検討する最近の研究において明らかにされてきたという。
2019年に小澤特任教授は、古典的な「二乗平均平方根誤差」を量子測定に拡張するために必要な要求を数学的に明らかにし、正しい測定の誤差が常にゼロであるという要求を「健全性」、誤差がゼロである測定は常に正しい測定であるという要求を「完全性」と呼んだ。ここでの誤差は、「真の値」(理想的な測定によって得られるべき値)と、「測定値」(実際の測定によって得られた値)の差として定義され、現代的な量子測定理論の枠組みでは、「真の値」を測定される物理量、「測定値」を測定直後のメーターの値を表す物理量として表現することが可能だという。
ただし量子物理学では、物理量が行列(作用素)で表されるため、「真の値」と「測定値」の差を表す物理量を「誤差作用素」と呼び、その二乗平均平方根を「量子二乗平均平方根誤差」とし、古典的な二乗平均平方根誤差の量子バージョンとしているという。
小澤特任教授は、誤差作用素に基づく量子二乗平均平方根誤差は一般に健全性を満たし、「真の値」と「測定値」が両立的な場合は完全性を満たすが、真の値と測定値が非両立的な場合には、完全性を満たさないことがあることを明らかにしていた。
古典物理学では、2つの物理量は常に同時にその値を決定することが可能だが、量子物理学では、同時にその値を決定することができない場合があり、前者の場合を両立的、後者を非両立的という。これは、それら2つの物理量に対応する行列の掛け算が交換法則を満たすか、否かという数学的条件に関係している。測定における「真の値」と「測定値」についても両立的な場合だけでなく、非両立的な場合があるのである。
そして小澤特任教授は「真の値」と「測定値」が非両立的な場合には、測定する状態を変化させることで隠れていた誤差が現れることを突き止め、誤差作用素に基づく定義を改良。健全性と完全性の両方の性質を持つ新しい定義を導き、「局所一様量子二乗平均平方根誤差」と命名したのである。
この新しい誤差概念は、従来の誤差概念と密接な関係を保っているため、従来の誤差概念をもとに導かれた「小澤の不等式」や、それを改良して新しく提案された「ブランシアードの不等式」もまったく式の形を変えることなく、この新しい誤差概念に対しても成立するという。つまり、この新しい誤差概念に対して成立する新たな不等式を導くという必要がないという。
そして今回の研究では、従来の測定方法では測定の誤差が出現することなく取り扱われる場合に関して、まず測定器に入力する初期状態をあるパラメータに関して掃引することで、隠れた誤差の出現が確認された。そして、パラメータ操作がシステマティックに行われ、量子測定の隠れた測定誤差が定量的に決定され、結果、物理的な考慮に相応した、量子測定の測定誤差が得られることが確認されたという。
-
測定される量子系の状態と、測定器の両者を考慮に入れた量子測定のモデル。入力する状態は測定器と相互作用した後に出力される。その一方、相互作用による測定器の状態の変化から測定結果がメーターに出力される (出所:共同プレスリリースPDF)
今回の実験では、測定器へ入力する初期状態をさらに既定のパラメータ値だけ変化させた上で量子二乗平均平方根誤差が計測された。それぞれのパラメータ値に対する量子二乗平均平方根誤差を求めた上で、パラメータ値を連続的に変化させ、最大値を求めることで局所一様量子二乗平均平方根誤差が得られるという。
-
実験配置図。実験用原子炉から取り出された中性子は、青の部分にあるポーラライザで状態「Ψ」に初期化される。次に、パラメータ掃引法を実行するために赤の部分にあるスピン回転器で初期状態をパラメータ値tだけ変化させて「Ψ(t)=U(t)Ψ」に変換する。緑の部分では、3状態法に必要な操作を行った後に、アナライザでスピン測定を行う。これらの測定によって得られたデータから、状態「Ψ(t)」における量子二乗平均平方根誤差の値を計算するのである (出所:共同プレスリリースPDF)
今回の実験では、初期状態に対する量子二乗平均平方根誤差の値はゼロだが、この測定は正確な測定ではないことが知られている。初期状態をパラメータ値「t」だけ変化させると、量子二乗平均平方根誤差の値は理論値で「2|sin t|」に変化する。実験データは、「0≦t<π」における12通りの値に対して高い精度で理論値が再現された。
また、パラメータ値を連続的に変化させることにより、最大値である局所一様量子二乗平均平方根誤差の値「2」が得られる。つまり、本来の初期状態における従来の定義による誤差の値ゼロに隠れていた誤差が、初期状態をパラメータ値tだけ変化させると誤差の値「2|sin t|」として現れる。よって、その最大値2が本来の誤差の値として得られるという小澤理論の予測が実験で検証されたとしている。
-
誤差測定の最終結果。図の実験パラメータは「パラメータt」に対して、「2t」に相当する。「0≦t<π」を満たす12通りのパラメータ値tについて、状態「Ψ(t)」における量子二乗平均平方根誤差がプロットされている。小澤理論の予測値「2
- sin t
- 」が高い精度で再現されているとした。この結果から、理論の予測通り、状態Ψにおけるこの測定の局所一様量子二乗平均平方根誤差が2であることが導かれる。グラフから、従来の定義による誤差の値ゼロに隠れていた誤差が、初期状態をパラメータ値tだけ変化させると、あたかも誤差の値2
- sin t
- として現れる様子が見て取れる。つまり、パラメータ掃引法による隠れた誤差2
- sin t
- の出現が確認され、その上で、この量子測定における隠れた測定誤差の値2を定量的に決定することができるのだ。(出所:共同プレスリリースPDF)
,A@alt属性はこちら|
今後、局所一様量子二乗平均平方根誤差の概念は、量子測定誤差の概念を確立し、あらゆる量子測定にあてはまる誤差の標準的定義として広く利活用されることが期待されると研究チームでは説明している。
とりわけ、「小澤の不等式」に代表される、近年著しく研究が進展しているハイゼンベルクの不確定性原理の精密な定量化に関する研究に確実な基礎を与えるという。重力波検出のような量子精密測定技術における誤差解析や、量子暗号や量子コンピュータのような量子情報技術の精度評価に広く応用されて、量子物理学の基礎と応用の進歩に広く貢献することが期待されるとしている。