大阪大学(阪大)は5月11日、最もシンプルなガラス状態である「剛体球ガラス」に対して圧縮およびシア(剪断)をかける数値シミュレーションをスーパーコンピューターを用いて実施した結果、さまざまな密度と異方性を持つ「ジャミング状態」の生成に成功し、その状態は力学的にギリギリの安定状態であり、同一の臨界性を持つことを明らかにしたと発表した。

同成果は、阪大 サイバーメディアセンターの吉野元准教授、中国科学院理論物理研究所のユリアン・ジン准教授(阪大 サイバーメディアセンター 招へい准教授)らの国際共同研究チームによるもの。詳細は、米科学雑誌「米科学アカデミー紀要(PNAS)」に掲載された。

球を最も密に箱に詰める方法を「最密充填」といい、古くから議論されてきた。17世紀に天体物理学者として有名なヨハネス・ケプラーが3次元での最密充填は「面心立方格子」であると予想。それから約400年後の1998年になり、トーマス・C・ヘイルズがこれを証明した。これに対し、「でたらめに」球を詰める実験をJ・ベナールとJ・メイソンらが1960年に行い、密度0.64付近でジャミング、すなわち「これ以上詰められない」の状態が得られることが見出されていた。

ジャミングとは、例えばパチンコ玉をざっと容器に流し込むと玉が、でたらめに、しかしぎっちりと詰まった状態になることで、ベナールとメイソンらはこれを「ランダム最密充填」と呼んだ。

その後の研究で、ランダムに詰めたジャミング状態は、圧縮を始める前の初期状態の作り方などによってさまざまな密度のものが得られることがわかってきた。そこで研究チームは今回、より詳細なジャミングについての研究を進めるため、スーパーコンピューターを用いて剛体球ガラスの大規模数値シミュレーションを実施したという。

その結果、圧縮だけでなく、体積は一定のままで箱を変形させるシア(剪断)によっても、さまざまなジャミング状態が得られることが見出されたとする。この現象は、粒子間に摩擦がある場合には知られていたが、摩擦がなくても実現することが今回示されたという。

  • ジャミング

    左は、ジャミング密度近傍にある高密度の剛球対ガラスのイメージ。右は3次元における最密充填構造である面心立方格子 (出所:阪大Webサイト)

さらに圧縮とシアを組み合わせて得られるさまざまな密度のジャミングがすべて共通した性質を持っていること、すなわち、これらすべてが力学的にギリギリの安定性を持つ「平均配位数」が6の状態にあること、ならびにさまざまな物理量が共通した臨界現象を示すことも判明したという。

  • ジャミング

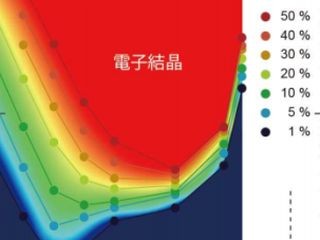
    圧縮とシアを組み合わせて得られるさまざまなジャミング密度。φjを持つ粒子配置でのデータが重ねられてプロットされている。粒子の直径は1。(左)粒子の中心から距離rにあるほかの粒子の平均的な数。さまざまなジャミング密度を持つ配置で共通する普遍的な振る舞いになっている。左のグラフから平均配位数は6であり、力学的にギリギリの安定状態にあることが見て取れる。また右図から、ほとんど接触しかけている粒子との距離は、普遍的な指数で特徴づけられるベキ分布に従っていることがわかる。これはある種の臨界状態にあることを示唆する (出所:阪大Webサイト)

なお、研究チームによれば、今回の成果により、結晶とは異なる、乱れたまま固体となったガラス(アモルファス構造)の基礎的理解が進むことが期待されるという。また将来的には、身近な工業材料や食品において重要なコロイドなど、高密度のソフトマターの制御にも役立つことが期待されるとしている。