東北大学ならびに科学技術振興機構(JST)は3月18日、非従来型コンピューターの1つである「確率論的コンピューター」の基盤をなす「確率ビット素子(疑似量子ビット)」として1秒間に1億回を超す状態更新の観測に成功したことを発表した。また、併せてこれまで着目されてこなかった動的磁化状態の「エントロピー」を考慮することで、その物理的起源が説明されることを示したことも発表された。
同成果は、東北大 電気通信研究所の金井駿助教、同・早川佳祐大学院生、同・大野英男教授(現・東北大総長兼電気通信研究所所長)、同・深見俊輔教授らの研究チームによるもの。論文は2本執筆され、米物理学会が刊行する学術誌「Physical Review Letters」ならびに「Physical Review B」に連携論文として掲載された。
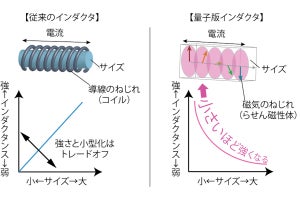
現在のコンピューターは、情報単位ビットにおいて、情報を0と1の2進法で扱い、計算や記憶などを行っている。それは、電子の持つ電荷(電気)とスピン(磁気)の2つの性質を同時に工学的に利用するスピントロニクスの原理を用いた「不揮発性磁気メモリ(MRAM)」であっても同じであるが、そこでは各状態には必ず「ゆらぎ」が存在し、ある一定の確率で、ゆらぎによる情報の喪失(物忘れ)が起こることから、その頻度を十分に低減させながら、ほかの性能を向上させるための研究が進められてきた。
2019年には東北大、米・パデュー大学の国際共同研究チームが磁気トンネル接合では、0と1の2状態間のエネルギー障壁が十分に高ければ「物忘れ」が抑制され、エネルギー障壁が低い場合は、2状態間の確率的な遷移を短い時間周期で繰り返すという性質が、量子コンピューターで用いられる情報単位である量子ビットと類似している点に着目し、量子ビットを模した確率ビットの開発に成功。1秒間に1000回程度ビット状態が書き換わる(物忘れをする)磁気トンネル接合素子を連結し、古典コンピューターが苦手とする最適化問題などを解く「確率論的コンピューター」の原理実証を行っている。
確率論的コンピューターとは、短時間で出力信号が確率的に変化し、かつ各ビットを電気的に相関させられる確率ビットを情報処理の基本単位とした、自然現象を効率よく再現するためのコンピューターで、量子コンピューターとは本質的には異なるものの、一定の類似性があることから、量子コンピューターと並んで非従来型のコンピューターとして注目されている。
また、熱ゆらぎによる状態の更新頻度が高いほど、計算の速度と精度の両方が向上するという特徴を持っているため、素早く「物忘れ」する磁気トンネル接合の開発が最重要課題の1つとなっていたという。
そこで研究チームは今回、電気通信研究所に附属するナノ・スピン実験施設の設備を用いて、「面内磁化容易軸」(磁化の向きやすい方向)を持つ磁気トンネル接合を作製し、1秒間に1億回を超える状態更新の観測に成功したという。
透過電圧を高速オシロスコープによって測定したところ、「磁気抵抗効果」により、平均8nsで0と1の状態間を高速に遷移していることが判明した。この結果は、従来の磁気トンネル接合の状態更新時間の世界最短記録980nsを大幅に短縮するものだという。
また、この高速化が磁化の熱ゆらぎに関する新しい理論的枠組みで説明できることも明らかにしたという。磁性体の磁化は磁場や「磁気異方性」の影響を受けて運動し、その挙動は絶対零度では決定論的運動方程式の「ランダウ・リフシッツ・ギルバート方程式」により導き出される一方で、有限温度では熱ゆらぎにより磁化の運動に確率性が生じるが、これはブラウン運動全般を記述する確率論的運動方程式の「フォッカー・プランク方程式」で記述されるとする。
今回の研究でも、この2つの方程式を組み合わせた確率論的運動方程式が用いられ、実際に観測されたナノ秒での状態間遷移の挙動が数値計算シミュレーションにより再現できることが確認されたという。
ある時刻で確定していた状態は、時間経過とともに徐々に状態の情報が不確かになり、最終的に状態を推定できなくなる。これが素子の「物忘れ」に相当するというが、この物忘れは不揮発性記憶素子では致命的な欠陥となるものの、確率ビットにおいては重要な駆動原理となり、これを言い換えると系の乱雑さ、すなわちエントロピーの増大と見なすことができるとしている。
これまでエントロピーという概念は、磁性体を扱う確率論的運動方程式では積極的に考慮されてこなかったというが、今回の研究から、エントロピーが動的に変化する様子を理論計算により調べられ、エントロピーの増大速度が従う方程式が導出されることとなった。導出された方程式から、面内磁化容易軸を持つ磁性体において、垂直方向の磁気異方性の絶対値が大きいほどエントロピーが急速に増大し、「物忘れ」が高速に進むことが説明されたのだという。
研究チームによれば、今回の研究で導かれた磁性体のエントロピーの時間変化に関する理論的枠組みは、学術的に広範な意味を有しているという。たとえば、磁性体には「歳差運動が高速であるほど、高速に磁化反転する」という経験則があるが、これは今回の方程式で統一的に説明することが可能だという。
また、エントロピーの時間変化を明示的に扱う今回の研究は、統計力学で百年以上続いたミクロな可逆性とマクロな不可逆性の関係に関する議論に対し、近年大きな進展をもたらした「ゆらぎの定理」などとも関連が深く、スピントロニクスと非平衡統計物理学を密接に関連させるきっかけとなることが期待されるともしている。
なお、今回の研究で開発された秒間1億回の状態更新を達成した素子に用いられている材料は、既存の半導路製造技術とも整合性が高いことから、高性能確率論的コンピューター実現の基盤となることが期待されると研究チームでは説明しているほか、今後は今回確立された超高速動作に関する理解と、これまでに構築されてきた演算技術、およびその基盤となる材料技術を向上させたつつ、高度に融合させることで、スピントロニクスを用いた高性能確率論的コンピューターの開発を加速していきたいとしている。