ISC 2015 - HPLを補うベンチマーク「HPCG」(前編)

TOP500のスパコンランキングは、「HPL(High Performance LINPACK)」というプログラムを実行する性能が使われている。HPLは「a₁₁*x₁＋a₁₂*x₂＋…a_1N*x_N=b₁、a₂₁*x₁＋a₂₂*x₂＋…a_2N*x_N=b₂、…　a_N1*x₁＋a_N2*x₂＋…a_NN*x_N=b_N」というN本の連立一次方程式を解くプログラムである。ここでaとbは値が決まっていて、これらの式を満たすxの値を求める。

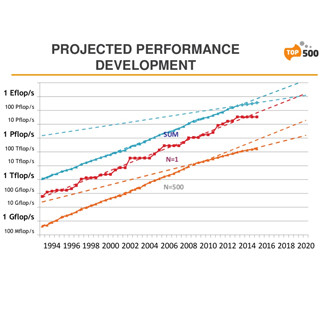
連立一次方程式を解くという問題は、科学技術計算ではよく出てくるので、20年あまり前にTOP500が始まった時以来、この問題が性能ランキングに使われている。

現実には疎行列となる問題が多い

例えば気象計算では、空間を3次元の格子状に区切り、1つの格子点の状態は隣接する周囲の格子点の温度や湿度などに影響されて変化するという形にモデル化する。つまり、格子点c_ijの次の時点の値は、c_ij自身とc_(i-1)jk、c_(i+1)jk、c_i(j-1)k、c_i(j+1)k、c_ij(k-1)、c_ij(k+1)の格子点の状態に依存する。しかし、それ以外の格子点の状態は直接的には影響しない。この例では7つの隣接格子点を使う計算であるが、本当のHPCGではもう少し複雑で、次の図に示すように、3×3×3の27要素の現在の値から中心の点の次の値を決めるという問題に対応して、各行の非ゼロ要素の数は27となっている。

行列Aのa_mn要素の値が、格子点mが格子点nに与える影響の大きさを表すとすると、隣接した格子点ペアに対応するa_mnはゼロでない値を持つが、大部分のa_mnはゼロとなる。例えば、i、j、kが100まであるとすると格子点の数は100×100×100で100万となる。そしてmとnは100万まであり、行列Aは100万×100万=1兆要素の行列となる。

しかし、HPCGのように1行に非ゼロ要素は27個しかないと、Aの大部分の要素はゼロで、非ゼロの要素はごく僅かという疎行列になる。

HPLは大多数の要素が非ゼロという密行列の問題であるので、LU分解という方法で、順次、変形を行いながら問題を解いていくが、巨大な疎行列のHPCGの場合は、LU分解でも解けるのであるが効率が悪い。このため、HPCGでは、解xの初期近似値x(0)を作り、Ax(0)を計算してbとの誤差を計算し、それを小さくするよう補正してx(1)を作るConjugate Gradientという反復型の計算方法を使っている。

疎行列ではメモリへの格納とアクセス法が問題

疎行列を扱う場合は、メモリへの格納やアクセスが問題になる。各要素が8バイトの倍精度浮動小数点数で、1兆要素の行列をそのまま格納するには8TBのメモリを必要とする。まあ、メモリをたくさん積んだサーバであれば、格納できなくはないが、モデルを詳細化して元の格子が1000×1000×1000になると、必要メモリは8Exaバイトとなり、とてもメモリには格納できない。

また、大部分の係数はゼロなので、そのために大量のメモリを用意するのは馬鹿らしい。疎行列を効率的に格納する方法は色々と考案されているが、HPCGでは、各行について、非ゼロ要素のある列番号とその要素の値を記憶する圧縮行格納方式(Compressed Row Storage、CRS)が使われている。

CRSのような格納法を使うことにより大きな行列を扱うことができるが要素をアクセスするには各行の非ゼロ要素のリストの先頭アドレスを求め、次にそのリストの中からアクセスする要素の列番号を見つけてから、値をアクセスする必要がある。また、要素が連続アドレスに格納されていれば、SIMDのLoad/Store命令があれば複数の要素をまとめて1命令で読めるし、キャッシュも効率的に使用できる。しかし、不連続に非ゼロ要素だけが格納されている場合は、それぞれをLoad/Store命令でアクセスすることになり、メモリアクセスの効率が悪い。

次の図は、HPCGの実行状況のプロファイルであるが、1番上の浮動小数点演算の使用率は平均で37%であるが、3番目のメモリアクセスの使用率は平均80.2%となっており、メモリアクセスがリミットとなっていることが分かる。