「GTC 2015 - 巨大電波望遠鏡「SKA」でパルサーを見つける」の関連記事 |
|---|
|
・【レポート】GTC 2015 - 巨大電波望遠鏡「SKA」でパルサーを見つける ・→ そのほかのGTC 2015の記事はコチラ |
GTC 2015で「Statistics of the Universe: Exa-calculations and Cosmology's Data Deluge」という発表があった。こんなアプローチがあるのかという点で興味深い発表であったので紹介する。
近年、ダークマターやダークエネルギーが見つかったが、それらが宇宙の進化にどのように影響を与えてきたかについては、まだ分からず、色々なモデルが提案されている状況である。どのようにしたら、どの説が正しいのかが分かるのであろうか?
観測できるすべての銀河を総当たり的に全部のペアを作って、その距離の分布を測ると、銀河の分布を表す指標になる。これを実測と、宇宙モデルに基づくシミュレーションから得られる距離の分布を示したものが右下の図で、両者は良く一致している。
|
|
すべての銀河のペアの間の距離を測り、その累積分布を求めると、モデルに基づくシミュレーションと実測は良く一致している |
次に、任意の3個の銀河を選んで三角形を作り、その最大の開き角と、角を挟む二辺の長さを取ってみる。
|
|
では、3つの銀河が作る三角形の開きの角θはどうであろうか? |
次の図は3つの宇宙モデルに対して、左は2銀河の距離、右は3銀河の開き角をプロットしたもので、前者はどのモデルでも実測の黒点と良く一致しているが、後者は一番上のモデルは良く一致しているが、2番目、3番目のモデルは左右の端ではずれが大きい。
|
|
3つの宇宙モデルで、2つの銀河間の距離の分布と3つの銀河が作る三角形の開き角の分布を比較した結果。黒が実測、青はモデルに基づくシミュレーション結果 |
この計算は、2銀河ペアの場合はN2であるが、3銀河の場合はN3回の計算が必要となる。また、2銀河ペアの場合は、ペアの距離の1次元のヒストグラムをとれば良いが、3銀河の場合は、開き角θとs、qの距離という3次元のヒストグラムになる。
|
|
ペアの数はN2だが3銀河の組み合わせはN3。ペアのヒストグラムは1次元だが、3銀河の開き角θとs、qのヒストグラムは3次元 |
観測されている銀河の数は2015年では10万個であるが、Large Synoptic Survey Telescopeの運用が本格化する2025年には100万個と10倍に増加する。3銀河の計算量はN3であるから、10万の場合は1Peta回であるが、100万になると1Exa回の計算が必要となる。
|
|
現在10万銀河でN3は1015であるが、2025年になるとLSSTが稼働を始め100万銀河が観測できるようになり、計算量は1018と1000倍になる |
3次元のヒストグラムでは3銀河を表す3つの座標値に対してビンを作り、個々のビンの範囲に入る3銀河が出てくると、ビンの値を＋1する。例えば、1つの銀河を固定して残りの銀河を変えた組み合わせは、次の図で白く書かれた3次元のヒストグラムの1つの面に対応する。なお、後の説明では、銀河座標としてはθ、s、qと書かれており、1つの銀河を固定したセットは1つの面にはならないと思われるが、ここでの説明としては、1銀河固定は分かりやすい説明である。
|
|
3銀河のヒストグラムは3次元となり、銀河座標1を固定しても、銀河座標0と2が作る白い箱で表わした1スライス分のヒストグラムが必要となる |
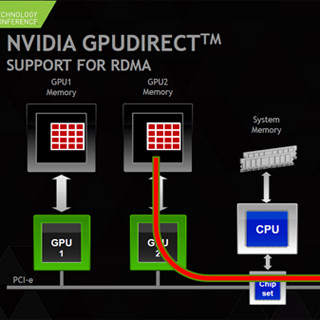
そして、GPUの1つのブロックに1スライス分のヒストグラムの計算を割り当てる。
|
|
GPUの1つのブロックに銀河座標1を一定とする一枚のスライスを担当させる |
1個のGPUでは能力が不足する場合は、3次元のボリュームをサブボリュームに分割して、それぞれを異なるCPUやGPUに担当させる。
|
|
3次元ヒストグラムをサブボリュームに分割して、それぞれにCPU/GPUを割り当てる |
銀河座標としてはθ、s、qと書かれており、それぞれの値が決まると、その値に対応するビンの内容を＋1する。しかし、多数のスレッドが並列に計算を行っているので、複数のスレッドのθ、s、qが同じビンを指し、同時にその値を＋1することが起こり得る。この場合のカウントが誤ることが無いように、アクセスを排他的にするatomicAdd命令を使っている。
|
|
多数のスレッドが並列に処理を行っているので、複数のスレッドの計算したθ、s、qが同じビンを指し、同じビンのカウントを同時に＋1することが起こり得る |
次の図では全体を5ビンとした粗い刻みの破線と、25ビンとした細かい刻みの実線の結果を示している。5ビンでは平均化されてしまって傾向が見えないが、25ビンでは傾向が良く分かる。このように、θ、s、qの刻みを細かくすると分解能が上がるので望ましい。また、多数のビンができるので複数のスレッドが同じビンにアクセスして待ち時間が発生することも少なくなる。一方、シェアードメモリの量が限られているので、ビンの数が多くなるとグローバルメモリを使わざるを得なくなり、性能が低下するという問題が出てくる。
|
|
ビンの刻みが粗いと、破線のグラフのように、カウントが平均化されて傾向が読み取れない。細かい刻みにすれば、実線のように傾向が良く分かる。一方、48KBしかシェアードメモリがないので、刻みを細かくするとシェアードメモリに入らず、性能がダウンしてしまう |
次の表はCPU(Xeon E5-1620 v2)とK40 GPUの実行時間を比較したもので、1万銀河の場合、CPUの場合は46.5時間と約2日かかるが、GPUでは2時間で計算できる。GPUはおおよそ20倍高速である。
|
|
Xeon E5-1620 v2 CPUとK40 GPUでの実行時間の比較。GPUは、CPUの約20倍の性能となっている |
CPUでは非常に時間が掛かるので、KD-treeという遠方の銀河をまとめる近似計算が使われるが、GPUを使えば、KD-treeよりも短い時間で厳密解が得られる。
|
|
5000銀河をCPUで計算すると5時間掛かるので遠方の銀河を纏めて計算するKD-treeが使われる。しかし、それでも22分かかる。一方、GPUを使えば、厳密解が14分で得られる |
結論であるが、宇宙論の研究もBig Dataを扱う時代になってきた。そして宇宙論の分野ではN3に比例するというスケーリングがうまく行かない問題がある。しかし、GPUはCPUより20倍速く、マルチGPU化が容易な問題であるので、エクサスケールになっても計算は可能であると結んだ。
|
|
宇宙論の研究もビッグデータの時代になってきた。しかし、GPUはCPUより20倍高速であり、マルチGPU化によるスケーリングの容易な計算であるので、エクサスケールの計算にも対応できる |
この研究にはSDSSのような望遠鏡や、次世代のLSST望遠鏡など、天空の広い領域を一度に観測し、遠方の宇宙の銀河のデータを得られる望遠鏡が必須であるが、そのデータから3銀河の作る三角形の形状を求めることで宇宙論の理論の正しさを検証できるというのはとても面白い。まったく異なるSKA電波望遠鏡でも観測データ処理にバックエンドとしてエクサスケールの巨大な計算能力を必要としており、確かに天文学はビッグデータの時代に入っている。
JAIST、「並行量子通信プロトコル」の完全な自動形式検証を実現
