東京大学(東大)は、スピン伝搬距離を決定する新たな手法を開拓したと発表した。これにより、困難だった正確なスピン伝搬距離の決定が簡便にできることから、量子情報やスピントロニクス素子の実現に大きく寄与することが考えられるという。

成果は、同大 物性研究所の大谷義近 教授、同 加藤岳生 准教授、同 新見康洋 助教らによるもの。詳細は「Physical Review Letters」に公開された。

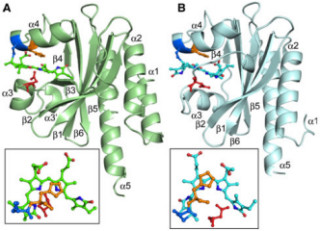
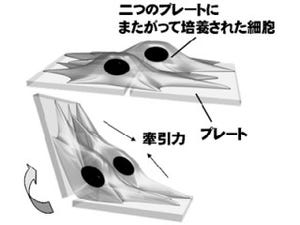
近年盛んに研究が行われている量子情報やスピントロニクスと呼ばれる分野では、電子がどれくらい遠くまでスピンの情報を伝搬できるか、つまりスピン伝搬距離が、将来のデバイス応用の観点からも重要な指標となっている。スピントロニクスの分野では、このスピン伝搬距離は通常強磁性体を用いて決定される。例えば図1に示されるように、2つの強磁性体を、スピン伝搬距離を調べたい物質で架橋し、その距離を変えることで、伝搬距離を求めることができる。しかし、この手法の場合、強磁性体の特性や強磁性体と調べたい物質との界面の特性にも依存するため、一度に決定すべき変数が増えてしまい、結果としてスピン伝搬距離を正確に決定することが難しくなる。

図1 図のように強磁性体から非磁性体(銀、銅、白金など)の左側に電流JCを流すと、強磁性体と非磁性体の電気化学ポテンシャル(μ)の違いから、非磁性体の右側には電流が流れていないにも関わらず、スピン角運動量のみの流れが生じる。この流れを純スピン流と呼ぶ。純スピン流は非磁性体の中で、スピン伝搬距離の範囲で緩和し、減衰していく。従来の方法では、スピン伝搬距離の範囲内で右側の強磁性体の位置を変えることで、スピン伝搬距離を決定することができる

また、図2のような強磁性体と調べたい物質との2層構造で強磁性共鳴曲線を測定し、それを詳細に解析することでもスピン伝搬距離が得られる。しかし、この場合、前者に比べて得られる値が1桁程度小さく、現在に至るまでどちらの手法で得られたスピン伝搬距離が正しいかをめぐって激しい論争が繰り広げられてきた。特に、スピン伝搬距離はスピントロニクスの分野で重要な物理現象の1つであるスピンホール効果の大きさを決定するのに不可欠であるため、この距離を正しく求めることは、基礎学問の立場からも応用上の立場からも非常に重要になっている。

図2 強磁性体/非磁性体2層構造で非磁性体のスピン伝搬距離を測定する時の模式図

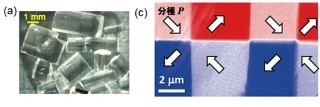
今回の研究では、これまでの強磁性体を使用するこれらの手法とは異なり、調べたい物質の細線の磁気抵抗を精密に測定するという比較的単純な手法で、スピン伝搬距離の決定が行われた。金属中の電子は、低温の極限になると不純物や格子欠陥の影響で、僅かに局在し、定在波を形成することが知られている(図3(a)-(c))。この現象は弱局在効果として知られており、実際に金属の抵抗が低温で僅かに大きくなる。

図3 (a)-(c)は定在波のイメージ図。(a)は左から右に進む波(実線)と逆方向に進む波(点線)は互いに干渉し合い、時間の経過とともに(1)→(2)→(3)→(4)→(1)のようになる。赤線が2つの波を足し合わせたもの。実際には、図(b)のように一部だけが振動しているように見える。これを定在波と呼ぶ。定在波の例として身近なところでは図(c)のような水面に立つさざ波がある。(d)金属中の電子は、低温の極限になると不純物(○印)に当たって、散乱される。電子には波の性質もあるため、不純物での散乱が弾性的であれば、図の実線のようなループを作ることができる。一方、電子の中にはそれとは全く逆の経路で進むものもある(点線)。そのような2つの状態が定在波を形成して干渉し合い、この範囲の中で電子は僅かに局在する。これを弱局在効果と呼ぶ。この効果によって、金属中の抵抗は僅かに低温で上昇する。しかし、図のような定在波を形成する確率は非常に小さく、通常の抵抗の1/1000くらいの大きさの抵抗変化しかない。そのため精密に抵抗を測定する必要がある

電子のスピン角運動量と軌道角運動量の相互作用が無視できるほど小さい物質であれば、通常この定在波は磁場を印加することによって、左回りと右回りの波が互いに異なる位相を獲得するために干渉が解け(図3(d))、図4左図のように抵抗が磁場とともに小さくなる。一方で、スピンと軌道の相互作用が強い物質の場合には、上記の局在効果を妨げ、図4右図のように、逆に抵抗が低温で僅かに小さくなる。この現象を弱反局在効果と呼ぶ。スピンにとっては、軌道角運動量との相互作用がデコヒーレンスの要因となる。今回の研究では、この弱反局在効果を用いてスピンの伝搬距離を求めた。

図4 スピンと軌道の相互作用が無視できるほど小さい場合には、図2で説明したように低温で抵抗が僅かに上昇する。磁場を印加することによって、図2のような干渉パターンは崩れてしまい、左図のような抵抗変化を示す。一方、スピンと軌道の相互作用が無視できない場合には、抵抗は低温の極限で僅かに減少する。これを弱反局在効果と呼ぶ。弱局在効果と同様に磁場を印加すれば、干渉パターンが崩れて、右図のような抵抗変化を示す

また、強磁性体を用いて得られる通常のスピン伝搬距離(図5左)と、弱反局在効果で得られる距離(図5右)が本当に同じものなのか、どのような関係で結びついているのかということはこれまで知られておらず、実験的に確かめた例はなかった。今回、研究グループは、スピンと軌道の相互作用が異なる銀、銅、白金の3種類の物質を用いて、2つの方法でスピン伝搬距離を調べた。この結果、図1の強磁性体を用いて得られるスピン伝搬距離と、弱反局在効果を用いて得られるスピンの伝搬距離は、約0.9(=√3/2)倍だけ異なること、この関係式を用いれば2つの手法で得られた値が定量的に一致することを確かめた。

図5 強磁性体を用いて得られるスピン伝搬距離(LS)と弱反局在におけるスピンの伝搬距離(LSO)はほぼ同じであるが、約0.9(=√3/2)倍ほど異なることを初めて実験的に確かめた

さらに、スピンと軌道の相互作用が比較的小さい銅を用いれば、その厚みを変えることによって、電気伝導率の大きさを変えることができる。銅のスピン伝搬距離の伝導率依存性を測定したところ、線形に変化することを初めて実験的に証明した(図6)。

図6 銅で測定されたスピン伝搬距離の電気伝導率依存性。銅の膜厚を変えることで、伝導率を変えることができ、スピン伝搬距離が伝導率に線形に変化することを初めて実験的に明らかにした。測定は、格子振動の影響が無視できる温度(4K)で行われた

今回の研究で使用した手法を用いれば、どんな物質のスピン伝搬距離も正確に求めることが、比較的簡単にできるようになるという。そのため研究グループでは、量子情報やスピントロニクスの分野では、スピンのデコヒーレンスの問題は非常に重要であるため、どのような物質・形状を用いれば、デコヒーレンスをより抑えられるかの指針を与えることができるようになるのではないかとコメントしている。