計算機(コンピュータ)を使うとき「文字列」(Strings)は、重要な要素だ。計算というと数値を考えてしまうが、文字列を処理できるようになって、計算機の用途は大きく広がった。そもそも、計算機の高級言語は、文字列で記述されたプログラムをソースコードとする。コンパイラであれ、インタプリタであれ、文字列で記述されたプログラムを実行するわけだ。
こうしたコンピュータ言語では、さまざまな文字列処理ができる。しかし、文字列処理は、アプリケーションでも行える。Excelのような表計算アプリケーションでは、数式で簡単な文字列処理が可能だ。プログラムを組まなくても、昔のBASIC言語程度の文字列処理ができる。
文字列の処理でよく利用されるパターンとして、「特定の文字列を含むかどうか?」というものがある。Excelには、文字列に特定の文字列が含まれているかどうかを調べる関数としてFINDとSEARCH関数があるのだが、見つからなかったときにエラーになるため、ちょっと扱いづらい。IF関数の中で使うなら、
=IF(ISERR(FIND("X",A1)),"No","Yes")
などとしてエラーかどうかを調べて、結果を判定する必要がある。ISERR関数がないと結果がエラーになってしまう。同様の目的にはIFERROR関数やISERROR関数も使えるが、IFERROR関数は表記が少し冗長になる(エラー時の値を指定する必要があり省略できない)、ISERROR関数は、対象が見つからなかった場合のN/Aエラーもエラーにならない。検査対象がセルならばいいのだが、LOOKUP系の関数などで対象が見つからなかった場合にエラーにならないため、間違いを見つけにくい。
文字列処理の場合、SEARCH/FIND関数を使うが、両者はワイルドカードの可、不可と大文字小文字の区別が異なる。ワイルドカードを使ったパターンならSEARCH関数を使うが、大文字小文字の区別がないという問題がある。FIND関数は、ワイルドカード文字は使えないが、大文字小文字を区別する。このとき、同一視させたければ、対象をUPPER関数で大文字化してしまえば、同一視させることができる。このため、FIND関数のほうが扱いやすい(それに関数名が短い)。
しかし、どちらも検索文字列を1つしか指定できないのでIF関数を使う場合には、複数の文字列を探すと数式が長くなってしまう。これはちょっと面倒だ。少し数式を短くする方法としてSUBSTITUTE関数を使う方法がある。この関数は対象から指定文字列を探し、置換する関数だ。
この関数を使うと、対象文字列をヌル文字列に置換することができ、対象文字列を消すことができる。このため、指定文字列「以外」の部分を取り出すことが可能だ。この結果を元の対象文字列と比較すると、文字列が消されたかどうかがわかる。また、対象文字列以外がわかるのなら、対象文字列だけを残すこともできる(写真01)。この関係を理解すれば、Excelの数式による文字列処理の記述が少しラクになる。SUBSTITUTE関数のいいところは、数式が複雑になってしまうIF関数を使う必要がなく、対象文字列が見つからなくてもエラーにならないところだ。Excel 2021やMicrosoft 365版Excelでは「スピル」と呼ばれる自動繰り返し機能が使える。詳しくは、Excelヘルプ「配列数式のガイドラインと例」を参照してほしい。
-
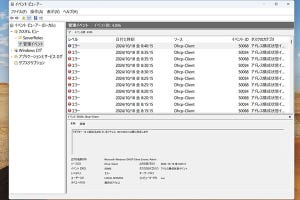
写真01: 複数キーワードの抽出にIF関数とSUBSTITUTE関数を使う例。キーボードショートカットから修飾キー(alt/ctrl/shift/winキー)を取り出すもの。FIND関数を使ってキーワードごとにIF関数で結果を判定したものを文字列連結演算子“&”で結合していく。これに対してSUBSTITUTE関数では、キーワードをすべて消した結果を使って、対象外の文字列を得て、これを消すことでキーワード部分を抽出している。処理内容に依存するがエラー処理が不要なためIF関数よりも記述が短くて済む場合がある
こうやって、文字列からパターンを取り出すことができれば、対象データをこれで分類分けすることが可能になる。このとき、Excelでは、ソート順をユーザーが指定できるので、結果を好きな順番で並び返ることもできる。それには、「データ」リボンの「並べ替え」のダイアログで「順序」のドロップダウンリストボックスで「ユーザー定義」を選択し、順番を定義すればよい。
今回のタイトルの元ネタは「弦理論」、あるいは「ひも理論」などと呼ばれる「String Theory」である。陽子や中性子、中間子など「ハドロン」と総称される粒子は、「点」ではなく空間的に広がりを持つ「振動」であるとしたのがString Theoryだが、1970年台に否定された。しかし1990年台に超対称性を取り込んで「超弦理論」(Super String Theory)として復活した。といっても全面的に認められたわけではなく、現実の観測を説明できておらず検証も困難なため、従来の立場からは「間違ってさえいない(Not Even Wrong)」(邦訳ストリング理論は科学か:原題物理学と数学。青土社)と言われることがある。