• ビットの喜び/Bit Delight

コンピュータは2進法で情報を扱う。なので、ときどきビットの操作を、行わねばならないことがある。このビット操作、単純なように思えるが、なかなか奥が深い。

単純な例としては、指定されたビット、たとえば、下から4番目のビットを1にするなら、対象と0b01000のOR操作を行えばよい。

Windowsで試すなら、PowerShellを使う。残念ながら、Windows付属のWindows PowerShell（Ver.5.1）では、2進定数を扱えないので、PowerShell（Ver.7.3）をインストールして使ったほうが便利だ。そのほか、繰り返し計算が面倒だがWindowsの「電卓」アプリのプログラマーモードでも2進数の計算はできる。

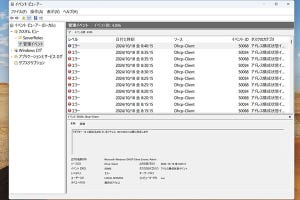
たとえば、下から4ビット目を1にするなら、下から4ビット目を1にしたマスク値0b000001000を定義しておく（$mに代入）。対象の数が0b010100011なら$xに代入して「$x OR $m」を計算する。PowerShellでは以下のようにする（写真01）。


$m=0b000001000
$x=0b010100011
[Convert]::ToString(($x -bor $m),2)

  • 写真01: 下から4番目のビットを1にするには、該当のビットだけを1にしたマスク値を作り、これと演算対象のビットでOR演算を行う。4行目がその結果。ここは表示位置を合わせるため演算式の先頭にスペースを13個入れている。「(' '*13)+」がその部分

“-bor”はOR演算、“[Convert]::ToString(数値,2)”は、2進数への変換である。PowerShellでは、数値の前に「0b」を付けることで二進定数を表現できるが、最上位ビットを1にしてしまうと、符号拡張されて負数になってしまうことがある。なので最上位ビットは、0になるように表記する。たとえば、0b10000000は、-128になってしまうが、0b010000000ならば128になる。必ず0b0を付けるようにすれば問題ない。

では「最も右側にある0を1にする」のような、意味は明確ではあるが対象により位置が変わる場合には、どうしたらいいのだろうか？ 簡単に思いつくのは、最も右側にあるゼロの位置を探す方法だが、そのためには条件判断やループを含むプログラムを書くしかない。しかし、これをビット演算だけで行う方法がある。それは「x OR (x+1）」という演算だ。PowerShellで書くなら、


$x=0b010100111
[Convert]::ToString(($x -bor ($x+1)),2)

となる（写真02）。最も右側にあるゼロの左側には、必ず最下位まで1が並んでいる。このため、1を足すと最も右側にあるゼロまで繰り上がりが起こりゼロが1になる。これと自分自身のORを取れば、1に変わったところは必ず1になり、そのほかのビットは変化しない。OR演算は、片方がゼロならもう一方はそのままになる。ビットの演算では、「0でないもの」は「かならず1」、「1でないもの」は「かならず0」になる。

  • 写真02: 最も右側にあるゼロ（この例では、下から4ビット目）を1に変更するには、ビットを探す必要はなく「X OR (X+1)」を計算するだけよい

なにか、ダマされたような気がしないでもない。これは演算自体が意味を語らないからである。「もっとも右側にある0を1にする」というのは、人間の考える「意味」である。演算はあくまでも演算なので意味は人間が見いだすしかない。

こうした演算と意味の関係を見いだすのは簡単ではないが、幸いなことに先人達がこうした発見を多数行ってくれているので、ありがたく利用させてもらえばよい。

演算で簡単に行える処理がある反面、ビット演算では、条件判断や繰り返しなどを使ったプログラムにしないと行えない処理もある。たとえば、最も右側（下位）にある連続した0の数を調べる問題だ。これは、古くからCTZ（Count Trailing Zeros）、NTZ（Number of Trailing Zeros）と呼ばれている。これは、「最も右側にある1の位置」（FFS:Find First Set。Setは1の意味）を求める問題でもある。末尾に並ぶ連続したゼロのすぐ左隣は1なので、その位置から1を引けば、ゼロの数になる。

コンピュータで何かの位置（順番）を表記するとき、ゼロを起点とすることが多い。というのは、後の処理が簡単になるからだ。だからFFSでゼロを起点として位置を表すと、それは、ゼロの数と一致する（図01)。数値「0b01011000」の場合、CTZの答えは3、FFSで起点を1とすれば4、起点が0ならば3である。

  • 図01: 最も右側にあるゼロの数を数える（CTZ。Count Trailing Zeros）ということは、もっとも右側にある1の位置を探す（FFS。Find First Set）のとほとんど同じ意味になる。なぜなら、最も右側にある連続したゼロの左側は必ず1になるからだ。この最も右側にある1の位置がわかれば、ゼロの数もわかる。

CTZを「バカ正直」に行うには、右端（下位）からビットを調べていき、1を見つけるまでの回数を数える。しかし、これも古くからの問題なので、さまざまなアルゴリズムを先人達が考えてきた。「Bit Twiddling Hacks」には、こうしたアルゴリズムが集められている。ページ中“Counting consecutive trailing zero bits”（連続する末尾のゼロ ビットを数える）がCTZのアルゴリズムである。

今回のタイトルネタは、Henry S. Warrenの“Hacker's Delight”(Addison-Wesley)である。2012年に第2版が出たが、国内では、2002年の初版のみ翻訳されている（邦題「ハッカーのたのしみ」）。この本には、いつかは使う必要に迫られる可能性が高いにも関わらず、普通では考えつかず、知識として仕入れるしかない演算やアルゴリズムが多数ある。