窓辺の小石(110) Scalable Vektor Analysis

SVG（Scalable Vector Graphics）は、W3Cで定義した2次元グラフィックス形式で、中身はXMLになっている。今回は、PowerShell Ver. 7.3.3を使って、SVGファイルを処理してみる（Windows PowerShell Ver.5.1ではエラーになる）。

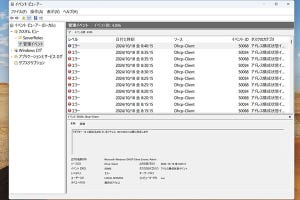
中身を見るだけなら、変数に読み込んで通常のオブジェクトのように扱えばよい。いま、カレントディレクトリに“MySVG.svg”があるとき、「$svg0=[xml](Get-Content .\MySVG.svg)」で変数$svg0に読み込むことができる（写真01）。

写真01: SVGファイルをXMLにキャストして読み込めば、簡単に内容にアクセスが可能になる

読み込まれたSVGは、.NETのオブジェクトである“System.Xml.XmlDocument”になっている。しかし、PowerShellからはオブジェクトに見えているので、ドット記法でタグをプロパティのように指定することが可能だ。反面、子要素のXMLタグと、svgタグのアトリビュートがともにプロパティになっている。

このSVGは、前回解説したmermaidから出力したもの。構造は、リスト01のようになっていて、「$svg0.svg.g.g.g.g[2]」で属性が「class="edgeLabels"」のgタグのブロックを取り出すことができる（リスト10行目に相当）。svgは、SVGのルートタグ、gはSVGのグループ化のタグだ。さらに、「$svg0.svg.g.g.g.g[2].g[0]」で、リストの10行目の内部にある最初のgタグを取り出せる。中身を調べるのであれば、これで十分だろう。

■リスト01



<svg...>
    <style> ... </style>
    <g class="svg-pan-zoom_viewport" ...>
        <style> ... </style>
        <g>
            <marker ...> ... </marker> ...
            <g class="root">
                <g class="clusters"> ... </g>
                <g class="edgePaths"> ... </g>
                <g class="edgeLabels"> ... </g>
                <g class="nodes"> ... </g>
            </g>
        </g>
    </g>
    <defs> ... </defs>
    <g id="svg-pan-zoom-controls" ...>  ... </g>
</svg>

では、今度は一部の要素を削除してみる。そのためには、.NET由来のxmldocumetオブジェクトとして扱い、XPATHを使う必要がある。PowerShellは、.NETのオブジェクトは自由に利用できる。

しかし、SVGは、XMLの名前空間を使っているため、XPATHでタグをそのまま扱うことができない。PowerShellからXML名前空間を使うには、以下のようにする。


$NS=New-Object -TypeName System.Xml.XmlNamespaceManager -ArgumentList $svg0.NameTable
$NS.AddNamespace('d', $svg0.DocumentElement.GetAttribute('xmlns'))

これで、“d”を使って名前空間で定義されたタグにXPATHでアクセスが可能になる。残念ながらページに余裕がないため「XML名前空間」や「XPATH」に関しては各自で調べてほしい。

タグを選択するには、


$svg0.SelectSingleNode('//d:defs' , $NS)

とする。

さて、mermaidから生成したSVGには、右下に拡大縮小のボタン用図形が含まれている（写真02）。リストでは、の部分である。これを削除してしまおう。属性を条件にしてXPATHで指定を行なう。

写真02: mermaidから出力したSVGには、ズーム用のボタン画像（写真中央下）が含まれているが、PowerShellを使って、これを削除することができる（写真右）


$y=$svg0.SelectSingleNode('//d:g[@id="svg-pan-zoom-controls"]',$NS)
$x.OwnerDocument.DocumentElement.RemoveChild($x)

とする。こうして不要な要素を削除したら、最後にXML形式で保存しておこう。理由はわからないが、saveメソッドはフルパスを指定しないと書き込みができない（エラーにもならない）。カレントディレクトリが入っている$pwdと、ファイル名をJoin-Pathコマンドでつなぎ「$svg0.Save((Join-Path $pwd "TestNextSVG.svg"))」とする。

XMLはテキストファイルなので、XPATHなどに堪能でなくとも、テキストエディタでも簡単に編集し、不要な部分の削除などが可能だ。だが、XMLを扱える言語なら、編集作業を自動化できる。

今回のタイトルネタは、ベクトル解析の書籍「Vector Analysis」（Edwin Bidwell Wilson, New York,1901）である。ベクトル解析は米国のGibbsの講義を元にした同書で確立されたと言われている。電磁気学でよく目にする∇演算子は四元数を考案したアイルランドのHamiltonが使い始め、∇とベクトルの外積となるcurl（回転）は、電磁気学の方程式で著名な英国Maxwellの提案である。Hamiltonの後継者TaitやMaxwellらは∇を「Nabla」（ナブラ）と命名したが、Gibbsはこの著書では∇演算子を「Del」（デル）と呼んでいた。大陸、新大陸の競合を垣間見るようだが、その反対側に位置する日本は、電磁気学やベクトルの表記では、どちらかというと大陸寄りである。