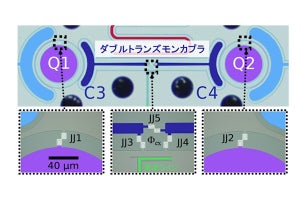
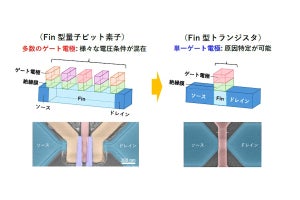
同手法の具体的検証として、物性分野で最も単純な模型である1次元ハイゼンベルグ模型に対する数値実験が行われ、数十量子ビットの量子コンピュータにおける同手法の挙動が、古典(既存)コンピュータによって再現された。

  • 今回の研究で確立された手法の概要

    (上)(a)量子系の情報(スピンなど)が時間経過とともに徐々に広がっていく様子。物理的に自然な仮定の下では情報の広がる速度には限界があり、Lieb-Robinson限界とはこのことを指す。(b)Lieb-Robinson限界の見方を変えたもの。(下)今回の研究で確立された手法の概要 (出所:QunaSys Webサイト)

その結果、同手法では鈴木-トロッター分解という従来手法と比べて、同じゲート数で約100倍精度良く量子系のダイナミクスを計算できることが判明したとするほか、最適化された量子回路を繰り返し用いることで、より長時間スケールのダイナミクスも効率よく計算できることが明らかにされたという。

今回の手法は、量子回路を設計するための計算の過程がLieb-Robinson限界で決まる小規模の量子系で閉じている点がポイントだという。それ故、目的の大規模な量子系のダイナミクスをあらかじめ正確に再現する必要がなく、小規模量子コンピュータまたは古典コンピュータを用いて効率よく計算する、コンパクトで高精度な量子回路を設計することが可能であり、大規模な量子系のダイナミクスの計算という、古典コンピュータでは困難な量子コンピュータの最も重要なアプリケーションの実現を加速するものと期待できると研究チームでは説明している。

  • 今回の手法の性能の検証結果

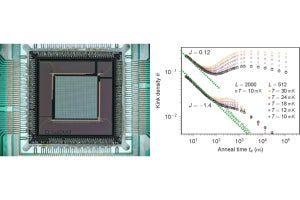
    今回の手法の性能の検証結果。(a)20～40量子ビットを持つ巨大な量子系に対して、20量子ビットの小規模量子系で最適化し、効率的な量子回路が設計された結果。(b)今回の手法で設計された量子回路を繰り返し利用し、長時間の量子系の時間変化が計算された結果 (出所:QunaSys Webサイト)

また今回の手法は、Lieb-Robinson限界という広範な量子系の持つ普遍的性質のみに依拠することから、大規模サイズ・長時間スケールのダイナミクスの効率的な量子計算に汎用的に役立ち、物性・材料・化学分野で関心の対象となるさまざまな量子物質に応用可能だと考えられるともする。

さらに、量子系のダイナミクスを計算する量子回路は単に量子系の時間発展を計算するだけではないという。エネルギー固有値・固有状態などの実応用の面において、重要なさまざまな性質を計算できる量子位相推定アルゴリズムなどの中でも多用されている。今後、今回の研究成果がさまざまな目的に利用されることで、より広範な量子アルゴリズムの効率化に貢献することが期待できるとしている。