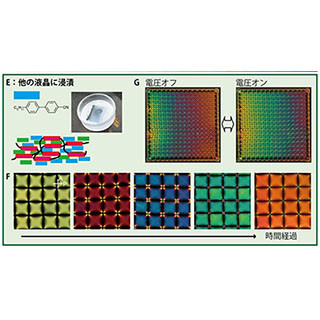
その結果、液晶に高電圧をかけて乱れた流れを起こすことで生成したトポロジカル欠陥が、電圧を切った後に動き回りながら次第に消えていく様子の観測に成功したほか、再結合やループ縮小・消滅といった線欠陥に特有の現象を捉えることにも成功したとする。

また、平行に近づくタイプの再結合に着目して、より詳細な解析が実施されたところ、2次元欠陥の運動と共通する性質と異なる性質の両方が明らかにされたという。

具体的には、3次元線欠陥が再結合の際にどのように接近するのかが調べられたところ、再結合時刻は欠陥同士の距離は√(t0-t)に比例することが判明。これは2次元の±1/2欠陥同士が近づき、ぶつかって消える対消滅の際に成り立つのと同様の法則であり、3次元線欠陥でも同じ法則が成立していたとする。

さらに、再結合に向かって接近してくる2本の線欠陥それぞれが、どのように運動しているのかが調べられたところ、2次元欠陥の対消滅の場合には、流れ場の効果により、+1/2欠陥が-1/2欠陥よりも速く動くという非対称なふるまいが起きるとされていたが、今回解析された線欠陥の運動は一見、2次元と同じように非対称だったが、注目している欠陥が周辺の領域から受ける影響を取り除いたところ、実際には2次元の場合とは異なり対称に運動していることが確認されたとする。

  • トポロジカルな線欠陥とその構造を表す概念図

    トポロジカルな線欠陥とその構造を表す概念図。実験で観察される線欠陥の中には、今にもつなぎ替えを起こそうとしているものもある(図左、破線の丸部分)。このつなぎ替え現象(再結合)の運動解析の結果、こうした線欠陥では「ねじれ欠陥」と呼ばれる構造(図右下)が自然に生じており、2次元液晶で見られる±1/2欠陥(図右上)とは異なることが判明した (出所:東大Webサイト)

研究チームでは、このような2次元と3次元の対称性の違いは、トポロジーとエネルギーの観点から議論できるとしている。2次元で±1/2欠陥はトポロジーとして区別できるのに対し、3次元では区別できない理由として、3次元では配向の回転軸がどの方向でも向ける点を挙げているほか、+1/2欠陥と-1/2欠陥の中間的な構造も取ることができ、+1/2欠陥から-1/2欠陥へと連続的に変形できるので、±1/2欠陥とその中間構造はすべてトポロジカルに等価となるとする。

  • 線欠陥の再結合とループ収縮・消滅の模式図

    線欠陥の再結合とループ収縮・消滅の模式図 (出所:東大Webサイト)

この中間構造の中には、近づく際に対称な運動をする構造(ねじれ欠陥)がある。今回用いられた液晶をはじめとして、ほとんどの液晶でこの構造はほかの構造よりもエネルギーが低い。つまり、トポロジーによって3次元でのみ許される構造が、エネルギー安定性のため、確かに実現すると考察することができ、実験的にも確認されたこととなった。トポロジカル欠陥の概念は液晶に限られたものではないが、同様の議論は液晶以外の同欠陥でも成り立つと考えられ、この「自発的対称性の回復」メカニズムには、液晶を超えた一般性があることが期待されると研究チームでは説明している。

  • 2次元で見られなかった対称性が3次元では回復することを表す概念図

    2次元で見られなかった対称性が3次元では回復することを表す概念図 (出所:東大Webサイト)

なお、トポロジカル欠陥は液晶だけにとどまらず、物理の広い領域に現れ、重要な役割を果たしているという。近年では生物系でも、細長い細胞や微生物などの集団的ふるまいが、液晶の理論やトポロジカル欠陥の概念で理解されるようになってきた。今回得られたトポロジカル欠陥の挙動に関する成果は、同欠陥が関わる広い学問領域に貢献する可能性があるとしている。