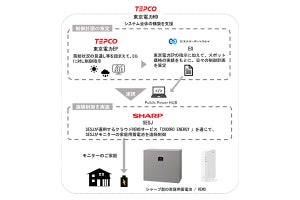
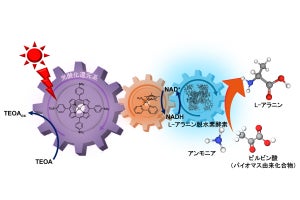
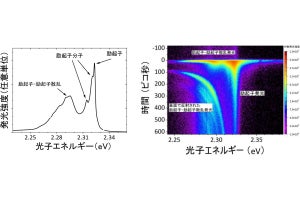
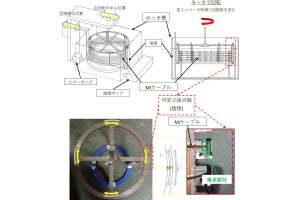
チューリングパターンは、分子の拡散と化学反応によって現れる、数理的にも最もよく知られているパターン形成メカニズムの1つで、平面上では、ストライプやドット状の静止したパターンを形成する。チューリングパターンを曲面上で調べたところ、平面では静止していたパターンが、ある特定の曲面上で伝播するということが発見された。これは、曲面の曲率によってパターン伝播現象が引き起こされることを意味するという。

これまでにも曲面上でチューリングパターンを調べた研究はあったが、そこでは静止したパターンが得られることが前提となっており、曲面上でのパターン伝播は過去の知見とは異なる新規な結果だとする。

  • 曲率によるパターン伝播

    曲率によるパターン伝播。平面では静止したチューリングパターン(上)が得られるが、曲面上では伝播するパターン(下)が得られた (出所:東大プレスリリースPDF)

この伝播現象を理解するために、軸対称曲面の場合に数値シミュレーションと理論的な解析が行われた。数値シミュレーションからは、「曲面の対称性」と「パターンの対称性」に依存してパターンの伝播が起こることが判明した。

  • パターン伝播と、曲面の対称性とパターンの対称性との関係

    パターン伝播と、曲面の対称性とパターンの対称性との関係。曲面がx=0(赤点線)で折り返して一致する鏡映対称性がなく、パターンが螺旋状の場合にはパターンが伝播する (出所:東大プレスリリースPDF)

続いてこの結果についての理論的な解析が行われ、チューリングパターンを含む反応拡散系一般に対して、伝播が起こる必要条件が導かれた。研究チームが見つけたパターンの伝播現象は曲面上だけで起こり、これまで知られている伝播パターンとは異なる新しい機構で生じていることがわかったという。

今回の研究により、曲率がパターンを伝播させる効果を持つことが示された。反応拡散系は物理・化学・生物学を含むさまざまな分野で数理モデルとして使われており、パターンは曲面上で豊富に見られることから、幅広い分野に対して、この伝播現象が観察されるだろうと期待されるとする。たとえば、生物学的文脈では、生体内の器官を形成する際に空間の位置を検知する機構として使われている可能性が考えられるという。また、伝播現象が曲面の対称性と関わっていることから、曲面を制御することにより伝播を調整するような応用が期待されるとしている。