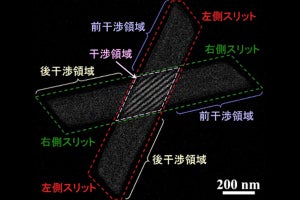
そして量子力学の世界においては、二重スリット実験などの粒子が干渉を起こす際に、2つあるスリットのどちらをどのように通過しているのか、という経路の問題が謎のままとなっているという。マクロの世界の感覚とは異なり、粒子がどちらの経路を通ったのかを観察してしまうと干渉が起きないためで、観察しないことが干渉を起こすための条件であり、異なる物理量の測定が両立しないことを表す「不確定性原理」により、経路の謎が守られてきたという。
しかし、「弱測定」と呼ばれる、干渉の明瞭度を保ちながら、何回もこの測定を繰り返すことによって、経路の情報も十分に得られるという仕組みを用いて、量子的な干渉を注意深く調整すると、その中間、つまり経路の情報と干渉との組み合わせを観測できるような状況を作り出すことが可能なこともわかってきたという。
その測定結果は、本来、粒子が1個1個独立に2つの経路にまたがって分布していることを示し、粒子が分割したり分身したりしているかのような振る舞いであるが、この測定結果は、厳密には統計集団での統計的なものであり、粒子1個1個を独立に測定した結果ではなかったとする。
そこでホフマン教授は2020年、弱測定の統計的ゆらぎを評価するための「フィードバック補償法」を考案。これにより弱測定の統計的ゆらぎ評価のために、ギャップを埋めることが可能となり、実際に2つの経路を持つ中性子干渉計に同手法を適用すると、2つの経路において観測された中性子の分割比の統計的なゆらぎは、無視できるぐらい小さいことが確認されたという。
-
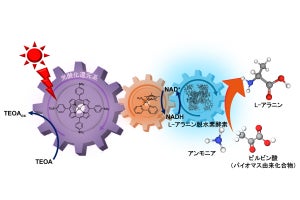
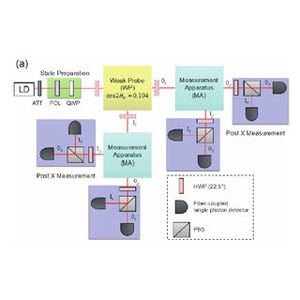
実験の概要図。x方向に向けたスピンを、経路1を通過した中性子のみz軸周りにα回転。干渉後の中性子のスピンを逆方向にβ回転。スピンがx方向に戻ったときの角度βが求める分割比となる (出所:広島大プレスリリースPDF)
しかしこの分割比は、測定結果、いい換えると粒子が最終的に検出される状況に依存しており、干渉が弱め合う場合は、1つの粒子が複数と負の粒子へ分割するような状況も起こり得るとしている。
なお、今回測定された中性子の分割比は、これまで弱値として知られている値と同じものだが、弱値が物理的にどのような意味を持つのか、まだ良くわかっていないという。そのため、今回の研究成果をもとに研究を進めることで弱値の謎の解明につながり、さらには広く一般的には量子力学の重ね合わせにおける問題の解明にもつながることが期待されるとしているほか、「小澤の不確定性関係」への応用も期待されるとしている。