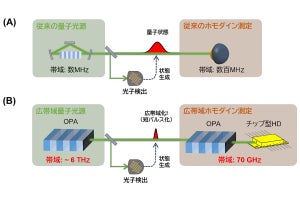
QUBOを効率的に解く富士通のデジタルアニーラ - ISC 2019

富士通のDAは全部の状態変化候補のエネルギー変化量とその採用確率を並列に計算する。そして、それぞれの選択肢の採用確率に比例してどの選択肢を選ぶかを選択する。おみくじに例えると、どの番号がでるかは、それぞれの番号の棒が引かれる確率があり(おみくじの場合は、どの棒も同じ確率であるが、この場合は棒ごとに引かれる確率が違う)、その確率で引かれた棒を選ぶ。

右のグラフは、横軸は探索のステップで、縦軸は系のエネルギーで、青線が富士通のDA、赤線が従来のアニーラである。赤線の方は不採用になって状態が変化しないステップも多いが、青線の方は、ほぼ毎ステップで最適な変化が加えられ、探索が速い。

N個の選択肢の採択確率に比例した確率で、候補を選択する。確率が高い選択肢が選ばれる確率が高いが、小さな確率の選択肢でもまれには選ばれる。右の図は赤が通常の方法で、空振りがあるので何ステップもエネルギーが変化しないことがあるが、富士通のDAはトライアルのステップ数は少ない

温度の高い状態では次の左端の図のように広い範囲を探索する。そして、温度が下がるに連れて中央、右端の図のように探索範囲は狭くなっていく。アニーリングでは全体の探索空間が非常に広いので、高い温度、中間の温度、低い温度での探索をうまく使い分ける必要がある。

温度の高い状態では左端の図のように広い範囲を探索するが。温度が下がるに連れて中央、右端の図のように狭い範囲を探索するようになる

富士通のDAでは同じ系のエネルギーE(x)で、複数の温度の状態(これをレプリカと呼ぶ)を作り、それぞれのれプリカで並列にMCMCで確率的な探索を行う。

そして、隣接する温度のレプリカの間で状態をスワップするパラレルテンパリングという方法を使っている。パラレルテンパリングでの状態のスワップはE(x)/Tkに比例した確率で決まる。パラレルテンパリングは統計物理では標準的に使われる技法であるという。

パラレルテンパリングで状態をスワップするとレプリカの温度が変わることになり、温度が高くなると局所最適解から脱出しやすくなる。

次の図では波形のようなグラフが4本あり、一番温度の低い青色の波形の振幅が大きいのは、T1が低い温度の場合E(x)/T1が一番大きいことを示している。そして、低温になるほど低エネルギーの状態の存在確率が高くなり、一方、高エネルギー状態にある確率が低くなる。

なお、レプリカの実装の詳細は明らかにされず、この図では4つのレプリカが書かれているが、実際はサポートされているレプリカの数は不明である。

局所最適解から抜け出すにはパラレルテンパリングをいう技法を使っている。パラレルテンパリングでは異なる温度のレプリカを複数持ち、レプリカの交換で温度を上げて局所最適解から抜け出しやすくしている

系の状態が平衡状態になっていない状態ではパラレルテンパリングは誤差が出るので、Burn-in時間と呼ばれる時間を待って、パラレルテンパリングを開始する。平衡状態になっていると、N個のサンプリングを並列に実行することにより、最適解を見つけるまでの時間を1/Nに短縮できる。

系が平衡状態になるようburn-in時間だけ待って、並列サンプリングを行う。平衡状態ではすべてのサンプリングが有効なので、並列サンプリング数に比例して性能が上がる

富士通は空振りなしのモンテカルロ法で性能を高め、さらに異なる温度のレプリカを計算するハードウェアを搭載して並列計算を行い性能を高めている。そして、右端の図のように複数の並列レプリカマシンを並べれば、それらのマシンの動作が独立であれば、確率的には並列度に逆比例して最適解を得るまでの時間を短縮できる。

富士通のDAは、各レベルで利用可能な並列性を利用している。可能な状態変化すべての採用確率を並列に計算し、複数のレプリカを並列に計算してパラレルテンパリングを行い、さらにコンパクトなので多数のマシンを並べることも可能である

巨大な筐体のD-Waveの量子アニールマシンを並べるのは現実的ではないが、デジタルアニーラなら極低温の冷凍機や強力な磁気シールドも必要なく、容易に多数のマシンを並べることができる。

ISC 2019で富士通ブースに展示されていたDigital Annealing Unit(DAU)

次のグラフは、左は32都市を巡回するセールスマンの都市訪問順序を最適化する問題で、横軸が最適化計算の繰り返し回数、縦軸は最適化の成功確率である。そして、赤線が富士通の空振りなしの方式、青線は通常のモンテカルロの場合を示す。この2本のグラフを比べると、富士通の方式は4桁程度、少ない繰り返しで最適解を見つけ出している。

右のグラフは、Max-cut G43というベンチマークでの富士通のDAと、通常のモンテカルロの比較である。このベンチマークでは富士通の方式は2桁弱繰り返し回数が少ないという結果になっている。

左は32都市のトラベリングセールスマン、右はMax-cut G43というベンチマークで、青線は通常のモンテカルロ、赤線は富士通のDAで繰り返し回数と成功確率のグラフ。富士通のDAはTSPで4桁、Max-cut G43では1桁少ない回数で最適解を見つけている

次の図は、Xeon E5-2686 CPUで実行させた場合と第1世代のDAUを使ったシステムとの実行時間の比較である。24都市の巡回セールスマン問題では、富士通のDAUでは10秒弱で最適解が得られているが、従来方式のXeonでの計算では、まだ、成功確率が上がり始めてもいない。右のグラフは1024-bitのスピングラス問題の計算結果で、どちらも、まだ、成功確率は低い状態であるが、富士通方式の方が2桁弱速い感じである。